什么是伪随机和真随机
1、真随机是指几率。比如百分之十七的几率,意味着你这次触发特殊事件是百分之十七的可能性,下次也是,每一次都是。如果你这次失败,下次依然保持在17%的可能性。几率意味着事件之间毫无联系。几率是所有事件相互独立,单次可能性保持在一定的几率范围。
2、伪随机是指程序生成的数字序列看起来随机,但实际上并非真正意义上的随机数。这种数字序列通常只是一些伪随机数,只有在特定条件下才会满足随机性的要求。举例来说,一个计算机程序可以生成一个伪随机序列,但它仍然可以被预测和计算机破解出来。在计算机科学和密码学中,伪随机数非常重要。
3、伪随机是指在计算机科学中,通过算法生成的、看似随机但实际上是有规律可循的序列。这些序列在表面上类似于真正的随机数,但在给定相同的初始条件或种子时,它们总是产生相同的输出。伪随机数的生成主要依赖于伪随机数生成器(PRNG),这是一种通过数学算法模拟随机过程的软件程序。
4、“真随机”就是我们现实世界中的随机,每次发生都是独立事件,概率不会相互影响。 比如一件事发生的概率是20%,不管是否发生,那么下次再发生的概率依然是20%。随机数生成器 是一个函数y=f(x),而 随机种子 则是变量x。所以一旦x和f(x)确定了,那么产生的随机数y也就确定。
5、真随机数是伴随着物理实验的,比如:抛硬币、掷骰子、电子元件的噪音、核裂变等,它的结果符合三大特性的。伪随机数伪随机数是通过一定算法,获得一个随机的值,并不是真的随机。伪随机又分为强伪随机数和弱伪随机数。强伪随机数:更加贴近真随机数,满足特性的。随机性和不可推测性,难以预测。
伪随机和真随机区别
1、真伪随机其实分别指的是几率和概率:伪随机是指概率。它出现得并不规律,但是大致上就是这么多次数。比如百分之十七,如果是每2000次为一周期,那么百分之十七意味着,尽管你不确定这340次究竟会什么时候出现,但2000次中必然出现340次,不多一次也不会少一次。貌似这就是伪随机了。
2、在程序原理层面,真随机指的是通过物理现象(如量子事件或特定设备的随机输出)获取不可预测的数据。而伪随机则是指通过算法生成看似随机但实质可预测的序列。具体实现上,常用方法是在系统时间等不可控因素作为种子,通过算法生成一连串随机数。
3、伪随机数伪随机数是通过一定算法,获得一个随机的值,并不是真的随机。伪随机又分为强伪随机数和弱伪随机数。强伪随机数:更加贴近真随机数,满足特性的。随机性和不可推测性,难以预测。弱伪随机数:满足随机性,可以预测。
4、随机性:完全紊乱; 不可预测性:从现有号码,无法推断下一个数字; 不可重复性:随机数之间没有重复。真随机数是伴随物理实验,例如:掷硬币、掷骰子、电子元件噪声、核裂变等,其结果符合三个特点。伪随机数是通过某种算法,获取随机值,不是真的很随机。
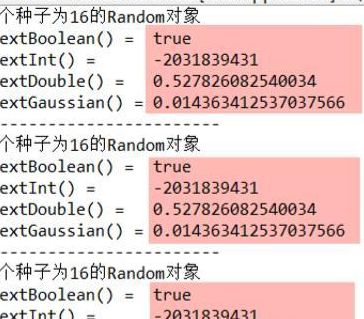
5、只要最初输入的数值(初值)不变,那么输出的值都会是同一个值,这就证明了这个数并不随机,只是看起来随机而已。 换句话说,只要这个随机数是由确定算法生成的,那就是赝随机数。
6、伪随机是指程序生成的数字序列看起来随机,但实际上并非真正意义上的随机数。这种数字序列通常只是一些伪随机数,只有在特定条件下才会满足随机性的要求。举例来说,一个计算机程序可以生成一个伪随机序列,但它仍然可以被预测和计算机破解出来。在计算机科学和密码学中,伪随机数非常重要。
如何找到伪随机数规律
1、找到伪随机数规律的方法有:直接法(Direct Method),根据分布函数的物理意义生成。缺点是仅适用于某些具有特殊分布的随机数,如二项式分布、泊松分布。逆转法(Inversion Method),假设U服从[0,1]区间上的均匀分布,令X=F-1(U),则X的累计分布函数(CDF)为F。
2、利用函数。类似把随机数的结果平方再除以100就可以增加比较小的数的出现概率。
3、一般地,伪随机数的生成方法主要有以下3种:(1) 直接法(Direct Method),根据分布函数的物理意义生成。缺点是仅适用于某些具有特殊分布的随机数,如二项式分布、泊松分布。(2) 逆转法(Inversion Method),假设U服从[0,1]区间上的均匀分布,令X=F-1(U),则X的累计分布函数(CDF)为F。
4、首先需要声明的是,计算机不会产生绝对随机的随机数,计算机只能产生“伪随机数”。其实绝对随机的随机数只是一种理想的随机数,即使计算机怎样发展,它也不会产生一串绝对随机的随机数。计算机只能生成相对的随机数,即伪随机数。
5、PRNG通常从一个初始值(种子)开始,然后应用一系列复杂的数学运算来生成一个看似随机的数列。这些运算通常是线性的,意味着如果给定相同的种子和运算步骤,PRNG将总是生成相同的数列。因此,尽管伪随机数序列在表面上看起来随机,但它们实际上是有规律可循的,可以在给定足够的信息时预测。
6、同时,伪随机数产生的起点,也就是种子可以通过热敏元件或者时间数据来产生,无法人为控制,使产生的数字序列更接近真随机状态。因此,要掌握到算法及其规律,并进行所谓预测,条件必须是指导算法和种子。
什么叫伪随机
伪随机是指程序生成的数字序列看起来随机,但实际上并非真正意义上的随机数。这种数字序列通常只是一些伪随机数,只有在特定条件下才会满足随机性的要求。举例来说,一个计算机程序可以生成一个伪随机序列,但它仍然可以被预测和计算机破解出来。在计算机科学和密码学中,伪随机数非常重要。
伪随机是指在计算机科学中,通过算法生成的、看似随机但实际上是有规律可循的序列。这些序列在表面上类似于真正的随机数,但在给定相同的初始条件或种子时,它们总是产生相同的输出。伪随机数的生成主要依赖于伪随机数生成器(PRNG),这是一种通过数学算法模拟随机过程的软件程序。
伪随机是指概率。它出现得并不规律,但是大致上就是这么多次数。比如百分之十七,如果是每2000次为一周期,那么百分之十七意味着,尽管你不确定这340次究竟会什么时候出现,但2000次中必然出现340次,不多一次也不会少一次。貌似这就是伪随机了。
在信息技术的世界里,伪随机这个术语指的是计算机和通信系统中用于生成的特殊序列。这些序列看似随机,但其实它们有着特定的生成规则,如直接法、逆转法或接受拒绝法等,确保了即使序列很长,也不会出现连续重复的情况。
伪随机,在计算机、通信系统中采用的随机,即这个码有多长都不会出现循环的现象。在计算机、通信系统中采用的随机数、随机码均为伪随机数、伪随机码,其生成方法有直接法、逆转法、接受拒绝法等。
在计算机、通信系统中我们采用的随机数、随机码均为伪随机数、伪随机码。
为什么游戏里的都是伪随机,做不出真随机?
技术难度的限制最后,技术上的限制也是导致游戏中只能使用伪随机的原因之一。在游戏中,需要生成大量的随机数,这需要消耗大量的计算资源和时间。而且,如果使用真正的随机数生成器来生成这些数字序列,那么它们可能会非常长,从而导致游戏的加载时间和运行速度变慢。
在应用层面,真随机意味着每次概率事件独立,不依赖于前次结果;伪随机则允许同一类事件之间存在一定程度的关联性,以平衡随机性与玩家体验。在抽奖系统等游戏中,引入伪随机算法旨在避免玩家遭遇极端幸运或倒霉的情况,从而提供更为平稳的游戏体验。
真随机,现实的触感想象一下,当你在一款游戏中,每一次攻击的暴击率都是由外部物理随机事件决定的,这种随机被称为真随机。它的真实性和不可预测性使得每一次结果都独一无二,就如同现实世界中的掷骰子。然而,实现真随机的成本较高,通常仅在需要高度公正性,如赌博游戏中才会采用。
因为,游戏开发者会在每个新游戏中使用一个不同的起始值,这样就能确保每个游戏的伪随机事件都是独立的,互不干扰。此外,小鸡游戏的算法中也包含了一些随机的元素,比如固定参数的选择、起始值的设置等等,这也会对游戏中的随机事件产生一定的影响。
什么是“随机”?教你分清“伪随机”和“真随机”
真随机是指几率。比如百分之十七的几率,意味着你这次触发特殊事件是百分之十七的可能性,下次也是,每一次都是。如果你这次失败,下次依然保持在17%的可能性。几率意味着事件之间毫无联系。几率是所有事件相互独立,单次可能性保持在一定的几率范围。
赝随机数算法(Pseudo-Random Number Generator,简称PRNG) 是计算机的一个术语——当然,它也可以被叫做“伪随机数算法”,只是为了方便与 游戏 中的“伪随机数”进行区分,本文中统一称作“赝随机数算法”。
伪随机是指程序生成的数字序列看起来随机,但实际上并非真正意义上的随机数。这种数字序列通常只是一些伪随机数,只有在特定条件下才会满足随机性的要求。举例来说,一个计算机程序可以生成一个伪随机序列,但它仍然可以被预测和计算机破解出来。在计算机科学和密码学中,伪随机数非常重要。