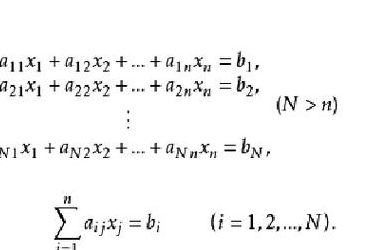什么是线性规划?
1、线性规划是一种优化方法,用于在给定的约束条件下找到最优解。在线性规划中,约束条件可以分为两类:紧约束条件和松约束条件。紧约束条件是指在某个可行域内,目标函数的值必须达到或超过某个阈值才能满足约束条件。换句话说,当目标函数的值低于这个阈值时,该解将不再被认为是可行的。
2、线性规划是一种数学优化技术,用于找到一组变量的最优解,这些变量在受到一系列线性约束条件的限制下,能够最大化或最小化一个线性目标函数。简单来说,线性规划就是在一组线性等式或不等式的约束下,求解一个线性目标函数的最优值。
3、线性规划是一种数学优化技术。线性规划是一种用于解决最优化问题的方法,特别是在需要处理多个变量和约束条件的决策问题中。这种方法主要通过找到一种最优的数值组合,满足一组给定的线性约束条件,来最大化或最小化一个线性目标函数。
在线性规划中什么是约束条件
1、郭敦顒线性规划的提法方法范围窄狭些,一般称为数学规划。数学规划中的约束条件是指决策变量与参数之间的关系,它是由所研究的特点所确定的(例如,生产过程中的性质,公司可得资源的数量,以及金融、市场、经济、政治、风俗方面的考虑)。这些关系应该定量地加以表示。
2、线性规划是一种优化方法,用于在给定的约束条件下找到最优解。在线性规划中,约束条件可以分为两类:紧约束条件和松约束条件。紧约束条件是指在某个可行域内,目标函数的值必须达到或超过某个阈值才能满足约束条件。换句话说,当目标函数的值低于这个阈值时,该解将不再被认为是可行的。
3、线性规划问题数学模型的标准型表达方法:约束条件都是等式,等式约束的右端项为非负的常数,每个变量都要求取非负数值。约束条件都是等式:在优化设计中,目标函数取决于设计变量,而设计变量的取值范围都有各种限制条件,如强度、刚度等。
4、约束条件是在平面内划分区域的,限制一个范围,可行区域是在条件下的,符合题目要求的一片区域。
项目的约束条件包括什么
这个约束条件包括时间约束、资源约束、质量约束。时间约束:项目需要在规定的时间内完成,因此时间是一个重要的约束条件。资源约束:项目需要使用各种资源,如人力、物力、财力等,这些资源的数量和质量都会对项目产生约束。
每一个项目都会在不同程度上受到范围目标、时间目标和成本目标的约束,这些限制条件在项目管理中通常被称为三项约束(triple constraint)。要想取得项目的成功,项目经理必须同时考虑范围、时间、成本这三个因素,由于这三个目标通常存在冲突,所以还要平衡这三者之间的关系。
项目的范围、时间和成本称为项目管理的三项约束。项日的范同是指项目实现的目标,或者是指项目发起人通过项目获得的产品或服务;项目的时间是指完成项目所需要的时间以及项目的进度安排;项目的成本是指完成项目所需花费的成本。通常这三个目标会存在冲突,项目经理的责任就是平衡三者之间的关系。
三重约束是:项目范围约束、项目时间约束、项目的成本约束。项目范围约束:项目经理在开始项目前一定要明确项目发起人的需求和期望。对于项目实际执行来说,范围可能会随着项目的进展而发生一些变化,从而与时间和成本等约束条件之间产生冲突。
影响因素和约束条件的区别
影响因素和约束条件的不同之处在于,前者可以通过人为努力改变,而后者是外部条件或内在限制,通常无法通过简单的努力来改变。
通用技术约束条件是对系统实施限制的因素,它们通常是不可人为调整的。这些约束条件对系统的操作或结果产生直接影响。 影响因素则指那些能够对系统目标产生显著影响的变量,这些因素通常是可以由人为决策或操作进行调整的。
区别如下:通用技术约束条件是对系统起限制作用的,并且是不可人为调节的;而影响因素是对系统的目标产生显著影响,是可以人为调节的因素。通用技术约束条件是起到限制作用的因素,对结果的作用更直接;而影响因素是对结果有间接作用的因素,其作用程度没有约束条件大。
对结果的作用更直接。影响因素是对结果有间接作用的因素,其作用程度没有制约因素大。制约,限制约束:受环境制约。是甲事物本身的存在和变化以乙事物本身的存在和变化为条件,则甲事物为乙事物所制约,如互相制约。通俗讲就是,限制、约束的意思。影响,指以间接或无形的方式来作用或改变。
充电功率大小是优化影响因素还是约束条件 充电功率大小是约束条件。根据查询相关资料信息,现有的研究大都是侧重于电网、电池等单一方面的影响,实际充电过程是受多方面因素的约束。充电功率通常指输电线路的充电功率,也称为无功功率。
桥梁选型与造型的约束条件主要有自然条件、经济条件、时间条件和技术条件四个方面。2桥梁选型桥梁选型取决于功能要求和约束条件,其与传统的桥型方案的确定过程相同。除自然条件、技术条件等因素外,不同的桥梁结构体系本身也存在着影响桥梁选型的若干因素。
在几何优化中,如何定义约束条件?
1、定义约束条件的步骤如下:确定设计变量:首先,需要明确要优化的设计变量。这些变量可以是长度、角度、面积等几何参数。确定约束条件的类型:约束条件可以是等式或不等式的形式。等式约束表示设计变量之间的关系,而不等式约束表示设计变量的取值范围。
2、首先,从数学模型的角度来看,几何优化主要关注于寻找一个最优的几何结构或形状,以满足一定的约束条件。它通常涉及到几何空间中的点、线、面等几何元素之间的关系和性质。而数值优化则更关注于找到一个最优的数值解,通常是在一定的目标函数下最小化或最大化某个指标。
3、在处理无约束优化问题时,优化条件更为抽象,主要关注在目标函数的可行域中寻找最优解的过程,该过程涉及到优化问题解空间的结构分析。需要通过一系列集合论的概念,如改善方向集、梯度集合等,理解优化问题的几何特性,从而构建几何意义上的必要与充分条件。