菱形对角线的性质
1、菱形的对角线性质有菱形的对角线长度相等、对角线互相平分、对角线的交点是中心、对角线的长度是半周长和对角线夹角为直角。菱形的对角线长度相等:菱形的两对对边平行,对角线相互垂直且长度相等。
2、菱形对角线的性质是菱形的两条对角线相互垂直,即交于中心点成直角。菱形的两条对角线相等,即对角线的长度相同。对于任意一条菱形对角线,它把整个菱形分成了两个全等的三角形。
3、对角线互相垂直且平分,并且每条对角线平分一组对角;在60°的菱形中,短对角线等于边长,长对角线是短对角线的√3倍。PS:这些在百度一搜一大把。40分有点多了。
菱形对角线和周长的关系
1、菱形的周长=4AB=2√(a^2+b^2)。
2、菱形和其他对角线互相垂直的四边形的面积等于两对角线乘积的一半)。菱形周长公式:由于菱形四边长都相等,因此周长等于四倍的边长即4a。菱形(rhombus)是特殊的平行四边形之一。有一组邻边相等的平行四边形称为菱形。
3、菱形四边等长,对角线互相平分且垂直,那么就存在对角线和边组成的直角三角形,设对角线长2a,2b,边长c,则a、b、c满足勾股定理。画个图就一目了然了。
4、.所以周长c=4a=根(m+n)。这与面积没关系呀! 若已知面积s与一条对角线长m,则可由mn=2s得n=2s/m,所以周长c=根(m+4s/m)=1/m×根(m的四次方+4s)。
5、菱形周长公式:由于菱形四边长都相等,因此周长等于四倍的边长即C=4a。有勾股定理:C=2√(c^2+d^2)。菱形的性质:菱形具有平行四边形的一切性质。菱形的四条边都相等。
菱形的对角线垂直吗
菱形的对角线垂直。菱形是一种四边形,它的所有边都相等长度,且对角线互相垂直。具体来说,菱形有两组相等的对边,其中每一组对边的长度相等,而且相对的两条边的夹角为90度。
垂直。菱形的对角线性质有:菱形的对角线互相垂直平分且平分每一组对角;菱形是轴对称图形,对称轴有2条,即两条对角线所在直线。由菱形的性质可知,菱形的对角线是互相垂直的。
菱形的对角线互相垂直。菱形的性质:菱形的对角线性质有:菱形的对角线互相垂直平分且平分每一组对角。菱形是轴对称图形,对称轴有2条,即两条对角线所在直线。
是的 对角线互相垂直平分的四边形是菱形。对角线互相平分且邻边相等的四边形是菱形。两组对边分别平行且一组邻边相等的四边形是菱形 两组对角分别相等,且一组邻边相等的四边形是菱形。
知道菱形边长怎么求对角线
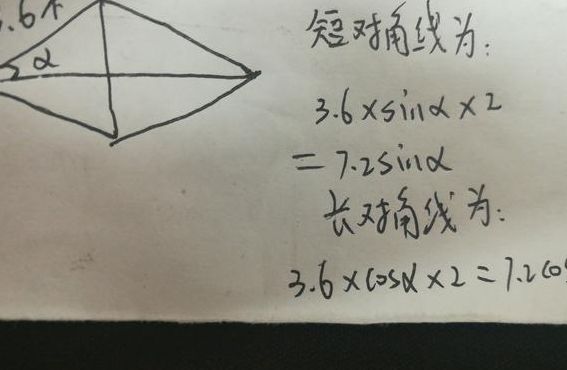
1、知道菱形边长求对角线的方法:菱形的边长是斜边,半条较短的对角线等于(10√3)/2=5√3根据勾股定理:半条较长的对角线=√[(10√3)-(5√3)]=15,较长的对角线=30。
2、菱形和其他对角线互相垂直的四边形的面积等于两对角线乘积的一半。
3、菱形的对角线的长度与菱形的形状有关。所以只知道菱形的四条边长还要知道其中一个角的大小,才能求出菱形的对角线的长度。
4、好简单哦~~~10*6=96 s菱形=96 因为两对角线乘积/2=s菱形 所以两对角线的一半的乘积等于24。
菱形的对角线有什么性质
菱形的对角线性质有菱形的对角线长度相等、对角线互相平分、对角线的交点是中心、对角线的长度是半周长和对角线夹角为直角。菱形的对角线长度相等:菱形的两对对边平行,对角线相互垂直且长度相等。
根据查询百度百科显示,性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的对角线互相垂直平分且平分每一组对角;菱形是轴对称图形,对称轴有2条,即两条对角线所在直线;菱形是中心对称图形。
菱形的对角线互相垂直,并且每一条对角线互相平分及平分一对对角。
互相垂直平分且平分每一组对角。菱形具有平行四边形的一切性质,其四条边都相等,其性质为互相垂直平分,且平分每一组对角。菱形是特殊的平行四边形之一,只要有一组邻边相等的平行四边形称为菱形。
性质:性质一:菱形的四条边相等。这是菱形最基本的性质,也是菱形与其他几何图形区别的重要标志。性质二:菱形的对角线相等。菱形的两条对角线相交于中心点,且相互垂直,因此对角线相等是菱形的重要性质之一。
菱形的所有性质如下:对角线互相垂直且平分,并且每条对角线平分一组对角。菱形既是轴对称图形,对称轴是两条对角线所在直线,也是中心对称图形。菱形是特殊的平行四边形,它具备平行四边形的一切性质。