蝴蝶定理公式
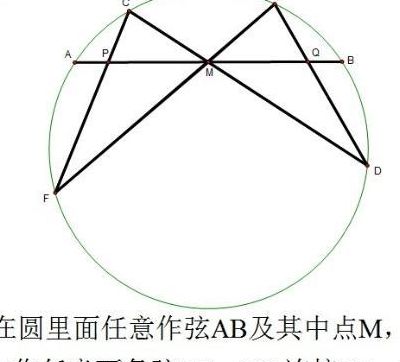
1、蝴蝶定理公式:XM=MY。蝴蝶定理(ButterflyTheorem),是古代欧氏平面几何中最精彩的结果之一。这个命题最早出现在1815年,由W.G.霍纳提出证明。平面几何指按照欧几里得的《几何原本》构造的几何学。也称欧几里得几何。
2、蝴蝶定理面积公式:DS/FS=DE/FC。蝴蝶模型面积公式:DS/FS=DE/FC。蝴蝶模型的面积公式是S1:S2=a2/b2。梯形蝴蝶定理是一个平面几何中的重要定理,由于该定理的几何图形形状奇特,形似蝴蝶,所以以蝴蝶来命名。
3、蝴蝶模型基本公式是AD:BC=OA:OC。蝴蝶模型又称梯形蝴蝶定理,是指在一个梯形中连接对角线后形成四个三角形。梯形蝴蝶定理是一个平面几何中的重要定理,由于该定理的几何图形形状奇特,形似蝴蝶,所以以蝴蝶来命名。
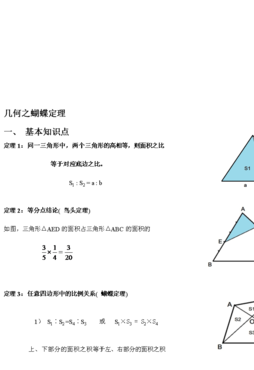
4、小学蝴蝶定理公式:任意四边形中的比例关系:S1∶S2=S4∶S3或S1×S3=S2×S4,上、下部分的面积之积等于左、右部分的面积之积。蝴蝶定理为我们提供了解决不规则四边形面积问题的途径。
5、任意四边形蝴蝶定理如下:小学蝴蝶定理公式 小学蝴蝶定理公式:任意四边形中的比例关系:S1∶S2=S4∶S3或S1×S3=S2×S4,上、下部分的面积之积等于左、右部分的面积之积。
蝶形定理
梯形蝴蝶定理是一个平面几何中的重要定理,由于该定理的几何图形形状奇特,形似蝴蝶,所以以蝴蝶来命名。计算公式有S3: S4=ab:cd、S1:S2:S3:S4等。在相似图形中适用,在实际问题中使用要看具体问题。
蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系。另一方面,也可以得到与面积对应的对角线的比例关系。
小学蝴蝶定理公式:任意四边形中的比例关系:S1∶S2=S4∶S3或S1×S3=S2×S4,上、下部分的面积之积等于左、右部分的面积之积。
该定理实际上是射影几何中一个定理的特殊情况。M作为圆内弦的交点是不必要的,可以移到圆外。圆可以改为任意圆锥曲线。将圆变为一个筝形,M为对角线交点。
该模型指的是小学数学梯形蝴蝶定理。蝴蝶模型是小学数学中的重点和难点,又称为梯形蝴蝶定理,是指在梯形中连接两条对角线后形成四个三角形。
蝴蝶定理是什么?
蝴蝶定理(Butterfly theorem),是古典欧式平面几何的最精彩的结果之一。这个命题最早出现在1815年,而“蝴蝶定理”这个名称最早出现在《美国数学月刊》1944年2月号,题目的图形象一只蝴蝶。
蝴蝶定理是古代欧氏平面几何中最精彩的结果之一。拓展知识:这个命题最早出现在1815年,由W.G.霍纳提出证明。而“蝴蝶定理”这个名称最早出现在《美国数学月刊》1944年2月号,题目的图形像一只蝴蝶。
蝴蝶定理最先是作为一个征求证明的问题,刊载于1815年的一份通俗杂志《男士日记》上。