对数定义域是什么?
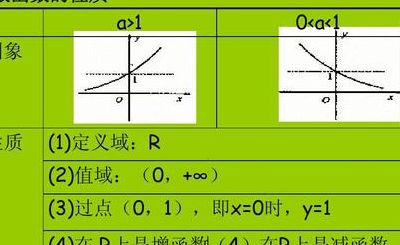
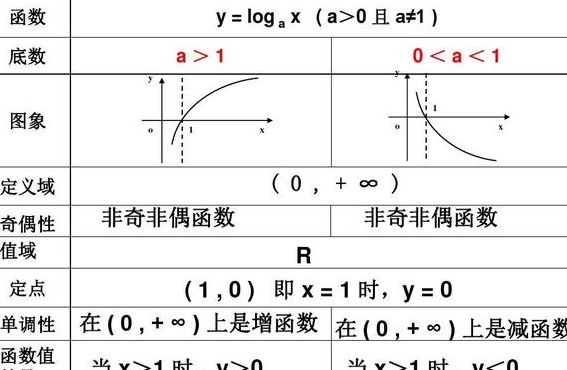
定义域是(0,+∞),即x0。一般地,对数函数以幂(真数)为自变量,指数为因变量,底数为常量的函数。对数函数是6类基本初等函数之一。
log的定义域是(0,+∞),即x0。函数y=loga(a>0,且a≠1)叫做对数函数,其中x是自变量。x的定义域是(1,+∞)。函数基本性质 过定点,即x=1时,y=0。
对数函数定义域是(0,+∞),即x0。一般地,函数y=logaX(a0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。
对数的定义域:x∈(0,+∞),值域:y∈R。对数函数是函数的一类,所以讨论对数函数的性质就是讨论函数的性质。
对数函数的定义域是:对数函数的真数g(x)>0;对数函数的底数f(x)>0,且f(x)≠1。
其中x是自变量,函数的定义域是(0,+∞),即x0。它实际上就是指数函数的反函数,可表示为x=ay。因此指数函数里对于a的规定,同样适用于对数函数。
对数函数怎么求定义域
1、对数的定义域:x∈(0,+∞),值域:y∈R。对数函数是函数的一类,所以讨论对数函数的性质就是讨论函数的性质。
2、所以定义域是(0,1)U(1,正无穷),即一切不等于1的正数。(2)首先作为对数的真数,x0,再因为根号要求log_3(x)=0,所以x=1,故定义域为[1,正无穷),即一切大于等于1的正数。
3、Log函数定义域即log后面的定义域>0,如y=logx,定义域即x>0,logx的值域为R。一般地,对数函数是以幂(真数)为自变量,指数为因变量,底数为常量的函数。
4、对数函数定义域为真数>0。比如log以3为底(x-1)的对数,让x-1>0,即定义域为{x|x>1}。幂函数定义域是底数≠0。比如y=(x-1)^2,让x-1≠0,即定义域为{x|x≠1}。
对数函数定义域是?
log的定义域是(0,+∞),即x0。函数y=loga(a>0,且a≠1)叫做对数函数,其中x是自变量。x的定义域是(1,+∞)。函数基本性质 过定点,即x=1时,y=0。
对数函数的定义域是:对数函数的真数g(x)>0;对数函数的底数f(x)>0,且f(x)≠1。
对数函数定义域是(0,+∞),即x0。一般地,函数y=logaX(a0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。
对数的定义域:x∈(0,+∞),值域:y∈R。对数函数是函数的一类,所以讨论对数函数的性质就是讨论函数的性质。