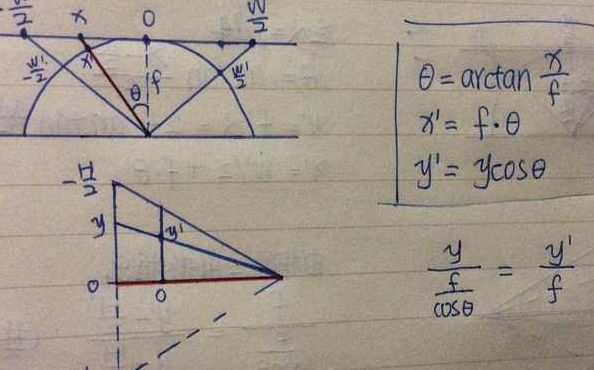
横轴等角切椭圆柱投影的特点
横轴等角切椭圆柱投影的特点:横轴、与一个经圈相切,与之相切的经线称之为中央经线、投影面是一个椭圆柱面、等角性质。
设想用一个椭圆柱横切于椭球面上投影带的中央子午线,按上述投影条件,将中央子午线两侧一定经差范围内的椭球面正形投影于椭圆柱面。将椭圆柱面沿过南北极的母线剪开展平,即为高斯投影平面。
高斯克吕格投影是一种横轴等角切椭圆柱投影。它是假设一个椭圆柱面与地球椭球体面横切于某一条经线上,按照等角条件将中央经线东、西各3度或5度经线范围内的经纬线投影到椭圆柱面上,然后将椭圆柱面展开成平面而成的。
高斯—克吕格投影是一种横轴等角切椭圆柱投影。
简称“高斯投影”,由德国数学家、物理学家、天文学家高斯拟定,后经德国大地测量学家克吕格加以补充,它是一种横轴等角切椭圆柱投影。
投影柱面方程需要写范围吗
投影曲线方程其实就是求的过交线垂直于xoy平面的柱面方程。在垂直于xoy平面的柱面方程柱面方程中,不含z,故两个方程联立消去z即可。
只要定义域不是函数的自然定义域,都应该写出来。
对啊。。这个想法其实很巧妙的。当一个方程不含有z的时候,在2维平面坐标系里就是一个曲线或是封闭的或是无限的或是什么什么的。总之是一个图形。
它们的方程都是二次的,统称为二次柱面。在空间直角坐标系中,只含两个变量的二次方程一般总表示一个二次柱面或者两个平面。柱面按照其几何特性可以分为以下3种不同类型的柱面:普通柱面、直圆柱面和二次柱面。
高等数学中,投影柱面方程是怎么回事?
对于给定的曲线,只要它不位于垂直于某一坐标平面的平面上,就有三个投影柱面。投影柱面与xoy面的交线叫做空间曲线在xoy面上的投影曲线.投影曲线方程|f(x)||x|为投影柱面的方程和所投影的坐标平面方程联立变成的方程组。
柱面方程的一般形式是x^2+y^2=r^2。柱面方程,即母线平行于坐标轴的,将两曲面方程联立,消去母线所平行的坐标轴的字母所得即为柱面方程。
柱面方程是z=√(x +y )与z =2x的交线(两方程联立求解)。柱面是直线沿着一条定曲线平行移动所形成的曲面,即动直线沿着一条定曲线平行移动所形成的曲面,动直线称为柱面的直母线,定曲线称为柱面的准线。
球坐标变换和柱面坐标变换的区别
1、球面坐标系中:z= 3*Sqrt[x^2 + y^2] &&(*与球面 改了球心位置,否则空图!,自己按需要再改参数*)x^2 + y^2 + (z - 3)^2 = 9, {x, -3。
2、就用柱面投影,经过柱面投影变换后的全景照片拼接处是连续的,不会出现折线。
3、柱面坐标使用平面极坐标和Z方向距离来定义物体的空间坐标,即r、thita、z.柱面坐标系就是平面极坐标系加上轴。(球坐标用离原点距离r、平面角thita、高度角fai来定义物体的空间坐标。
为什么垂直于xoy的柱没有投影面积
对于前者,其投影在XOY面上变成一条圆线,也就没有二重积分了,即没有面积了,所以曲面积分为0。。对于后者,其投影到YOZ面,圆柱面的前后两侧投影重叠了,相当于计算时无形中少算了一部分,所以得分成前后两侧进行计算。
你这是在求曲面积分的时候,分析曲面的投影吧?题中的圆柱(没有顶和底,只有侧面)在xoy面投影确实是一条曲线——圆,但是不包括圆的内部,所以分割后的小段上面积微元为零,从而曲面积分为零。并不是说投影是个零。
圆柱面直线的投影没有积聚性。圆柱面、圆锥面和圆球面的投影均没有积聚性。投影法的基本概念之一当平面垂直某一投影面时,平面在该投影面上的投影为直线。
柱坐标投影方法有哪几种,怎么算?
1、柱坐标通过定义某点在 XY 平面中距 UCS 原点的距离,在 XY 平面中与 X 轴所成的角度以及 Z 值来定位该点。绝对坐标:是以点O为原点,作为参考点,来定位平面内某一点的具体位置,表示方法为:A(X,Y)。
2、确定投影带:投影的方法,在比例尺 1:5万-1:50万图上采用6°分带,对比例尺为 1:1万及大于1:1万的图采用3°分带。换算,就用三角函数将球体上的坐标(经纬)换算为投影的圆柱坐标。转化为地图方里坐标。
3、在一维的数轴上,你只有x轴,x=1就是一个点啦。那在二维的xoy坐标系上,你的x=1就可以从(1,0)这点自由向上向下移动,形成一条平行于y轴的直线啦。这个直线就是x=1,和y没关系。
4、圆柱坐标(ρ,θ,z)是.圆柱坐标系上的点的表达式。
5、柱坐标系中的三个坐标变量是 r、φ、z。与空间直角坐标系相同,柱坐标系中也有一个z变量。