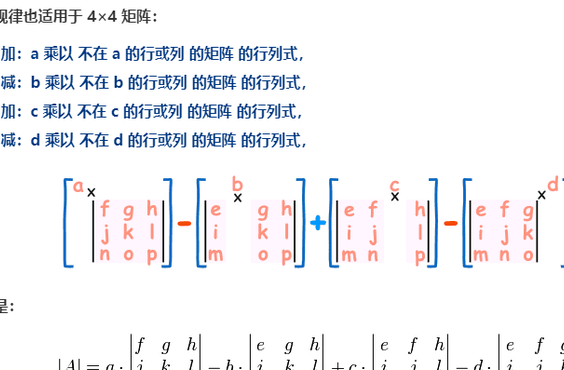
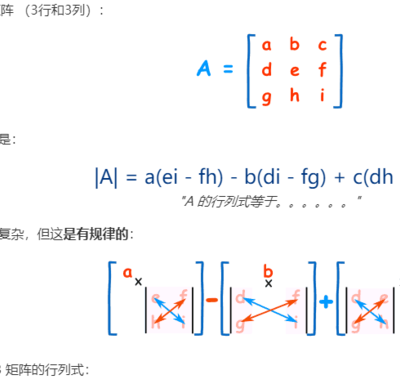
矩阵行列式怎么算
行列式计算基本公式是:D=A=detA=det(aij)。行列式在数学中,是一个函数,其定义域为det的矩阵A,取值为一个标量,写作det(A)或| A |。
单位矩阵的行列式为 1 ,与之对应的是单位立方体的体积是 1。行列式的某一行(列)中所有的元素都乘以同一数k,等于用数k乘此行列式。在消元的过程中,行列式不会改变,如果有行交换的话,符号不同。
行列式的乘法公式其实是矩阵的乘法得来的,即 |A||B| = |AB|;其中 A.B 为同阶方阵,若记 A=(aij),B=(bij),则|A||B| = |(cij)|,cij = ai1b1j+ai2b2j+...+ainbnj。
一个n×n的方阵A的行列式记为det(A)或者|A|,一个2×2矩阵的行列式可表示如下:把一个n阶行列式中的元素aij所在的第i行和第j列划去后,留下来的n-1阶行列式叫做元素aij的余子式,记作Mij。
计算2阶行列式是线性代数中最简单的行列式计算之一。2阶行列式通常表示为:| a b | | c d | 其中,a、b、c、d是矩阵中的元素。
矩阵行列式
伴随矩阵除以原矩阵行列式的值就是原矩阵的逆矩阵。如果二维矩阵可逆,那么它的逆矩阵和它的伴随矩阵之间只差一个系数,对多维矩阵不存在这个规律。伴随矩阵对不可逆的矩阵也有定义,并且不需要用到除法。
矩阵行列式是指矩阵的全部元素构成的行列式,设A=(aij)是数域P上的一个n阶矩阵,则所有A=(aij)中的元素组成的行列式称为矩阵A的行列式,记为|A|或det(A)。行列式的意义是变换后,空间的膨胀系数。
也就是说伴随矩阵就是A逆矩阵中所有元素均乘以一个lAl,并且是三阶矩阵。所以计算伴随矩阵的行列式的方法就是将A逆三行每行都提出一个lAl后即可。
矩阵行列式的性质
1、行列式的性质 行列式A中某行(或列)用同一数k乘,其结果等于kA。行列式A等于其转置行列式AT(AT的第i行为A的第i列)。
2、性质1行列式与它的转置行列式相等性质2互换行列式的两行列,行列式变号性质3行列式的某一行列中所有的元素都乘以同一数k,等于用数k乘此行列式性质4行列式中如果有两行列元素成比例,则此行列式等于。
3、行列式是线性代数中的基本概念之一,它是个由行和列组成的方阵的特殊值,反映了矩阵在行列方面的特性。行列式与零的关系行列式等于零的情况主要发生在方阵的行或列中存在全零的情况。
4、扩展资料 性质6:把行列式某一行的元素乘以同于个数后加到另一行的对应元素上,行列式不变.行列式在数学中,是一个函数,其定义域为det的矩阵A,取值为一个标量,写作det(A)或 | A | 。
矩阵的行列式计算方法是什么?
所以计算伴随矩阵的行列式的方法就是将A逆三行每行都提出一个lAl后即可。
按斜线计算A*E*I,B*F*G,C*D*H,求和AEI+BFG+CDH。再按斜线计算C*E*G,D*B*I,A*H*F,求和CEG+DBI+AHF。行列式的值就为(AEI+BFG+CDH)-(CEG+DBI+AHF)。
第行列式的计算利用的是行列式的性质,而行列式的本质是一个数字,所以行列式的变化都是建立在已有性质的基础上的等量变化,改变的是行列式的“外观”。
矩阵的行列式怎么求?
1、所以计算伴随矩阵的行列式的方法就是将A逆三行每行都提出一个lAl后即可。
2、将第n行依次与第n-1行、第n-2行、...、第2行交换,一共交换n-2次;...将第n行与第n-1行交换1次。以上共交换了1+2+3+...+(n-1)=n(n-1)/2次。
3、方法1:把两个行列式,都分别求出来,然后相乘。
4、应用矩阵运算法则,二三阶的可以用主对角线乘积的和减去副对角线乘积的和。加竖线,就是对矩阵A,求行列式行列式|A|是一个计算结果,是1个数字,而矩阵A是一组数据(n行n列)。
矩阵的行列式是什么?
1、A矩阵的行列式(determinant),用符号det(A)表示。行列式在数学中,是由解线性方程组产生的一种算式其定义域为nxn的矩阵 A,取值为一个标量,写作det(A)或 | A | 。行列式可以看做是有向面积或体积。
2、矩阵的行列式就是以矩阵的元素为元素的行列式。所以只有行数与列数相等的方阵才有对应的行列式。
3、在矩阵 中,任取k行和k列 ,位于这些行和列的交点上的 个元素原来的次序所组成的k阶方阵的行列式,叫做A的一个k阶子式。
4、矩阵的行列式等于0说明矩阵中所有元素不都为0。不等于0是行列式的值不是0,是通过计算的来的一个不为0的数字。矩阵行列式是指矩阵的全部元素构成的行列式。