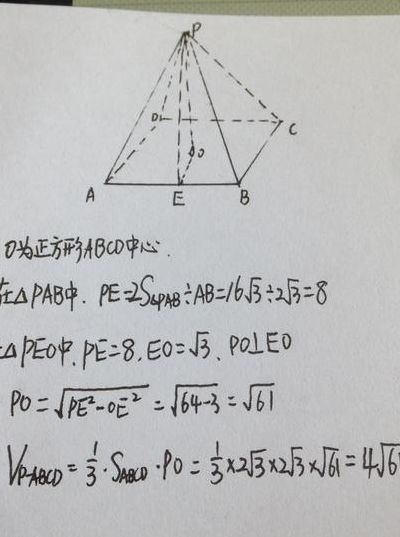什么是正四棱锥?
1、正四棱锥的定义:底面是正方形,侧面为4个全等的等腰三角形且有公共顶点,顶点在底面的投影是底面的中心。三角形的底边就是正方形的边。
2、正四棱锥是一种具有四个等边三角形和一个正四边形为底面的锥体,它的侧棱长度相等且与底面垂直。
3、四棱锥是指由四个三角形和一个四边形构成的空间封闭图形,而正四棱锥,则是底面为正方形,四个三角形为全等三角形而且是等腰三角形。
四棱锥长什么样
四棱锥是指由四个三角形和一个四边形构成的空间封闭图形,而正四棱锥,则是底面为正方形,四个三角形为全等三角形而且是等腰三角形。
四棱锥是一种几何图形,它的形状是由底部为四边形和四条侧棱组成的。这种图形可以被描述为一个具有四个三角形和一个四边形的立体形状,其中三角形是四棱锥的侧面,而四边形是底部。
四棱锥是一种具有四个棱和一个尖顶的多面体。它的性质取决于底面形状和棱的长度和角度。四棱锥的体积和表面积可以根据相应的公式进行计算。在现实生活中,四棱锥有着广泛的应用,从古代的金字塔到现代的建筑设计。
正四棱锥体积公式
正四棱台 V=H/3[S1+S2+√(S1S2)]非通用公式(s1是上底的面积,s2是下底的面积)。
棱锥的体积公式都是:V=1/3*h*S底。
V=(1/3)Sh。正四棱锥体积的计算公式为:体积=(1/3)×底面积×高其中,底面积指的是正四边形的面积,可以根据底边长和高计算得出。高指的是从底面上一顶点到底面上一顶点到底面上与另一顶点连线的垂直距离。
正四棱锥的每一条棱都相等吗?
底面都是正多边形;顶点在底面的射影是底面的中心;各条侧棱都相等;4各个侧面都是全等的等腰三角形。
正四棱锥是一种具有四个等边三角形和一个正四边形为底面的锥体,它的侧棱长度相等且与底面垂直。
其中,正四棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高)。
正四棱锥性质:(1)正四棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高)。
几棱锥各棱长相等指的是:几棱锥的所有侧面组成的多边形都是相等的,也就是说生面的棱长、面积以及顶角都相等。在这里,顶角是指几棱锥的顶点所在的角,它与几何体的上下底面接触。
球心到顶点的距离等于到面距离的两倍长,即外切球球心是内切球球心的半径的两倍长。
有关正四棱锥
正四棱锥各侧棱相等,各侧面都是全等的等腰三角形等。
正四棱锥是一种具有四个等边三角形和一个正四边形为底面的锥体,它的侧棱长度相等且与底面垂直。
正四棱锥的底面是正方形。正四棱锥是一种四面体形状的立体图形,由一个正方形底面和四个等边三角形组成,底面和顶点之间的连线称为棱。
正四棱锥定义:底面是正方形,侧面为4个全等的等腰三角形且有公共顶点,顶点在底面的投影是底面的中心。底面是正方形,顶点在底面的射影是正方形的中心。三角形的底边就是正方形的边。
正四棱锥高与底边的关系是相等,正四棱锥底面是正方形,侧面为4个全等的等腰三角形且有公共顶点,顶点在底面的投影是底面的中心。底面是正方形,顶点在地面的射影是正方形的中心。三角形的底边就是正方形的边。