共轭复数是什么?
1、两个实部相等,虚部互为相反数的复数互为共轭复数(conjugate complex number)。(当虚部不等于0时也叫共轭虚数)复数z的共轭复数记作zˊ。
2、所谓的共轭复数,是指一个数的实部相等,虚部互为相反数的数。所有的数都是复数,所以,实数的共轭为本身;含有i的复数的共轭只需将i前的正负号变一下就行了。
3、什么是共轭复数:共轭复数是两个实部相等,虚部互为相反数的复数互为共轭复数(conjugate complex number)。
4、zˊ=a-bi。共轭复数所对应的点关于实轴对称(详见附图)。
5、共轭复数是指两个实部相等,虚部互为相反数的复数互为共轭复数。当 虚部不为零时,共轭复数就是实部相等,虚部相反,如果虚部为零,其共轭复数就是自身。复数z的共轭复数记作z(上加一横),有时也可表示为Z*。
6、共轭复数:通常指的两个实部相同,虚部相反的的两个复数,叫做这两个复数的共轭复数。
复数的共轭复数
1、复数z的共轭复数是z=a+bi(a,b∈R)。共轭复数,两个实部相等,虚部互为相反数的复数互为共轭复数。
2、共轭复数的定义是若z=a+bi(a,b∈R),则 z的共轭=a-bi(a,b∈R)。两个实部相等,虚部互为相反数的复数互为共轭复数。两个复数:x+yi与x-yi称为共轭复数,它们的实部相等,虚部互为相反数。
3、共轭复数,两个实部相等,虚部互为相反数的复数互为共轭复数(conjugate complex number)。当虚部不为零时,共轭复数就是实部相等,虚部相反,如果虚部为零,其共轭复数就是自身(当虚部不等于0时也叫共轭虚数)。
4、复数的共轭复数很简单,只要把虚部取反即可,例如:复数5/3+4i的共轭复数是5/3-4i。两个实部相等、虚部互为相反数的复数互为共轭复数。
5、的复共轭(complex conjugate)。基本概念:共轭复数,两个实部相等,虚部互为相反数的复数互为共轭复数。当虚部不为零时,共轭复数就是实部相等,虚部相反,如果虚部为零,其共轭复数就是自身。
6、共轭复数 两个实部相等,虚部互为相反数的复数互为共轭复数。复数z的共轭复数记作zˊ。根据定义,若z=a+bi(a,b∈R),则 zˊ=a-bi。共轭复数所对应的点关于实轴对称(详见附图)。
共轭复数怎么求?
若复数z=a+bi(a,b属于R)则复数z的共轭复数为z(截)=a-bi。
复数的共轭复数很简单,只要把虚部取反即可,例如:复数5/3+4i的共轭复数是5/3-4i。两个实部相等、虚部互为相反数的复数互为共轭复数。
当 时,方程无实根,但在复数范围内有2个复根。复根的求法为 (其中 是复数, )。由于共轭复数的定义是形如 的形式,称 与 为共轭复数。另一种表达方法可用向量法表达: , 。
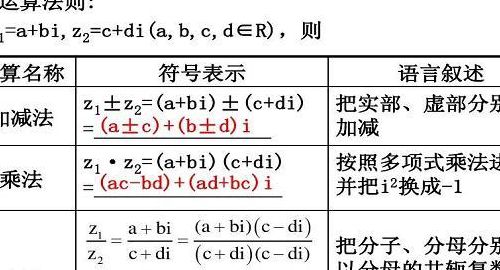
求法:(一)、加法法则:设z1=a+bi,z2=c+di是任意两个复数。两者和的实部是原来两个复数实部的和,它的虚部是原来两个虚部的和。两个复数的和依然是复数。即 (a+bi)±(c+di)=(a±c)+(b±d)i。
共轭复数的性质 (1)︱x+yi︱=︱x-yi︱;(2)(x+yi)*(x-yi)=x2+y2=︱x+yi︱2=︱x-yi︱2。
共轭复数
1、共轭复数,两个实部相等,虚部互为相反数的复数互为共轭复数(conjugate complex number)。当虚部不为零时,共轭复数就是实部相等,虚部相反,如果虚部为零,其共轭复数就是自身(当虚部不等于0时也叫共轭虚数)。
2、复数的共轭复数很简单,只要把虚部取反即可,例如:复数5/3+4i的共轭复数是5/3-4i。两个实部相等、虚部互为相反数的复数互为共轭复数。
3、共轭复数 两个实部相等,虚部互为相反数的复数互为共轭复数。复数z的共轭复数记作zˊ。根据定义,若z=a+bi(a,b∈R),则 zˊ=a-bi。共轭复数所对应的点关于实轴对称(详见附图)。