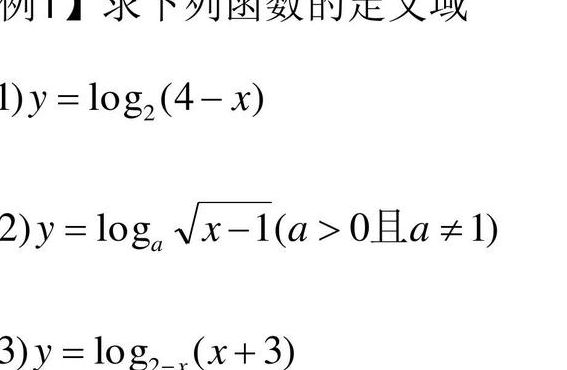log函数的定义域是什么?
1、对数函数的定义域是大于0的实数集合,即$(0, +\infty)$。对数函数的基本形式为$y = \log_{a}{x}$,其中$a$是底数,$x$是自变量。对数函数的定义要求$x$必须大于0,因为对数函数是基于指数函数的反函数,而指数函数的定义域是全体实数,但其值域是大于0的实数。
2、对数函数的定义域是:对数函数的真数g(x)>0;对数函数的底数f(x)>0,且f(x)≠1。一般地,函数y=logaX(a0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。其中x是自变量,函数的定义域是(0,+∞),即x0。
3、lg函数的定义域:(-∞,1)。一般地,函数y=logaX(a0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。
4、log函数是指数函数的反函数。它的性质如下: 定义域:log函数的定义域是正实数集合,即x 0。 值域:log函数的值域是实数集合。 单调性:log函数是严格递增函数,即随着x的增大,log(x)也随之增大。 零点:log函数的零点是1,即log(1) = 0。
5、log的定义域是:y=logaX。一般地,对数函数是以幂(真数)为自变量,指数为因变量,底数为常量的函数。对数函数是6类基本初等函数之一。其中对数的定义:如果ax=N(a0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数,其中a叫做对数的底数,N叫做真数。
6、定义域是(0,+∞),即x0。一般地,对数函数以幂(真数)为自变量,指数为因变量,底数为常量的函数。对数函数是6类基本初等函数之一。其中对数的定义:如果a^x=N(a0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数。
对数函数的定义域是什么?
函数的定义域是(0,+∞),即x0。对数函数是6类基本初等函数之一。其中对数的定义:如果ax =N(a0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数,其中a叫做对数的底数,N叫做真数。
定义域是(0,+∞),即x0。一般地,对数函数以幂(真数)为自变量,指数为因变量,底数为常量的函数。对数函数是6类基本初等函数之一。其中对数的定义:如果a^x=N(a0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数。
对数函数的定义域是:对数函数的真数g(x)>0;对数函数的底数f(x)>0,且f(x)≠1。一般地,函数y=logaX(a0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。其中x是自变量,函数的定义域是(0,+∞),即x0。
对数函数的定义域
函数的定义域是(0,+∞),即x0。对数函数是6类基本初等函数之一。其中对数的定义:如果ax =N(a0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数,其中a叫做对数的底数,N叫做真数。
对数函数的定义域为所有正实数。具体来说,对于形如f=log_a的对数函数,其定义域是x大于0的所有实数。对数函数的自变量必须为正数,这是因为对数函数的定义是基于正数的幂运算的逆运算。因此,对数函数的定义域不包含任何负数或零。
定义域是(0,+∞),即x0。一般地,对数函数以幂(真数)为自变量,指数为因变量,底数为常量的函数。对数函数是6类基本初等函数之一。其中对数的定义:如果a^x=N(a0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数。
对数函数的定义域是:对数函数的真数g(x)>0;对数函数的底数f(x)>0,且f(x)≠1。一般地,函数y=logaX(a0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。其中x是自变量,函数的定义域是(0,+∞),即x0。
对数函数的定义域知识点
一般地,我们把函数y=logax(a>0,且a≠1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞),值域是R。在涉及到对数函数时,一定要注意定义域,即满足真数大于零;求值域时,还要考虑底数的取值范围。
对数函数的定义域是:对数函数的真数g(x)>0;对数函数的底数f(x)>0,且f(x)≠1。一般地,函数y=logaX(a0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。其中x是自变量,函数的定义域是(0,+∞),即x0。
对数函数定义域是(0,+∞),即x0。一般地,函数y=logaX(a0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。其中x是自变量,函数的定义域是(0,+∞),即x0。它实际上就是指数函数的反函数,可表示为x=ay。
对数函数是指以某个正实数为底数的指数函数的反函数。例如,以2为底数的指数函数y=2^x的反函数就是以2为底数的对数函数y=log2x。对数函数的一般形式为y=logax,其中a是底数,x是实数。对数函数的定义域是指该函数可以输入的所有实数的集合。
对数函数log的定义域是所有正实数,即(0, +)。对数函数log以某个正实数a(a1)为底,记作logx,其定义是:对于所有正实数x,存在一个唯一的实数y,使得a^y = x。这里的a被称为底数,x被称为真数,y则被称为以a为底x的对数,记作y = logx。
对数函数的定义域是正实数集,即x的取值范围是大于0的实数。对数函数的基本概念 对数函数是指以一个正数作为底数,另一个正数作为真数,求使其等于真数的指数的函数。