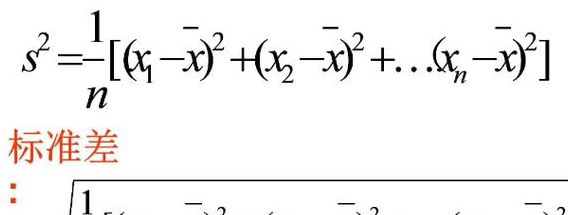样本方差的公式是什么
1、样本方差公式为:S = 样本方差是衡量样本数据离散程度的一个重要指标。其计算公式如下: 公式表达:样本方差公式中的S代表样本方差,n为样本数量,X为样本数据,均值是样本数据的平均值。表示求和,即计算所有样本点与均值的差的平方和。
2、样本方差公式:E(S^2)=DX。先求出总体各单位变量值与其算术平均数的离差的平方,然后再对此变量取平均数,就叫做样本方差。样本方差用来表示一列数的变异程度。样本均值又叫样本均数。即为样本的均值。在许多实际情况下,人口的真实差异事先是不知道的,必须以某种方式计算。
3、样本方差与总体方差的关系公式是样本方差等于总体方差除以n,总体方差的计算公式分母是n,样本方差的计算公式分母是n-1,抽取样本的目的是推算出总体的信息。先求出总体各单位变量值与其算术平均数的离差的平方,然后再对此变量取平均数,就叫做样本方差。
样本方差的计算公式
1、样本方差公式:E(S^2)=DX。先求出总体各单位变量值与其算术平均数的离差的平方,然后再对此变量取平均数,就叫做样本方差。样本方差用来表示一列数的变异程度。样本均值又叫样本均数。即为样本的均值。在许多实际情况下,人口的真实差异事先是不知道的,必须以某种方式计算。
2、样本方差公式为:S = 样本方差是衡量样本数据离散程度的一个重要指标。其计算公式如下: 公式表达:样本方差公式中的S代表样本方差,n为样本数量,X为样本数据,均值是样本数据的平均值。表示求和,即计算所有样本点与均值的差的平方和。
3、样本方差与总体方差的关系公式是样本方差等于总体方差除以n,总体方差的计算公式分母是n,样本方差的计算公式分母是n-1,抽取样本的目的是推算出总体的信息。先求出总体各单位变量值与其算术平均数的离差的平方,然后再对此变量取平均数,就叫做样本方差。
样本方差公式.极差公式。平方差公式。快
其中,x表示样本的平均数,n表示样本的数量,xi表示个体,而s^2就表示方差。平方差:a-b=(a+b)(a-b)。文字表达式:两个数的和与这两个数的差的积等于这两个数的平方差。此即平方差公式 标准差:标准差=sqrt(((x1-x)^2 +(x2-x)^2 +...(xn-x)^2)/n)。
方差:,其中,x表示样本的平均数,n表示样本的数量,xi表示个体,而s^2就表示方差。平方差:a-b=(a+b)(a-b)。标准差:标准差=sqrt(((x1-x)^2 +(x2-x)^2 +...(xn-x)^2)/n)。
方差公式是s=[(x1-x)^2+(x2-x)^2+(xn-x)^2],标准差公式是sqrt[(x1-x)^2+(x2-x)^2+(xn-x)^2]。平方差的公式为a-b=(a+b)(a-b),表示两个数的和与这两个数的差的积等于这两个数的平方差。方差是衡量随机变量或一组数据离散程度的指标。
方差是统计学中的关键概念,它衡量数据点与平均数之间的偏差程度,用公式D表示,计算方法是各个数据与平均数差的平方之和除以数据数量。记为s^2,即s^2 = (1/n) * Σ(xi - x)^2,其中x为样本平均数,n为样本量,xi为每个个体数值。
样本方差的公式
样本方差公式为:S = 样本方差是衡量样本数据离散程度的一个重要指标。其计算公式如下: 公式表达:样本方差公式中的S代表样本方差,n为样本数量,X为样本数据,均值是样本数据的平均值。表示求和,即计算所有样本点与均值的差的平方和。
样本方差的公式是:S = * Σ^2 / n。其中,S代表样本方差,n是样本数量,μ是样本均值,X是样本中的各个观测值,Σ表示求和。该公式用于计算一个样本数据集中各数值与其均值之间的离散程度。
样本方差公式:E(S^2)=DX。先求出总体各单位变量值与其算术平均数的离差的平方,然后再对此变量取平均数,就叫做样本方差。样本方差用来表示一列数的变异程度。样本均值又叫样本均数。即为样本的均值。在许多实际情况下,人口的真实差异事先是不知道的,必须以某种方式计算。
样本方差与总体方差的关系公式是样本方差等于总体方差除以n,总体方差的计算公式分母是n,样本方差的计算公式分母是n-1,抽取样本的目的是推算出总体的信息。先求出总体各单位变量值与其算术平均数的离差的平方,然后再对此变量取平均数,就叫做样本方差。
方差计算公式两种:S^2=(1/n)、S=(X2-平均数)^方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。
样本方差公式-样本方差的计算公式?
样本方差公式为:S = 样本方差是衡量样本数据离散程度的一个重要指标。其计算公式如下: 公式表达:样本方差公式中的S代表样本方差,n为样本数量,X为样本数据,均值是样本数据的平均值。表示求和,即计算所有样本点与均值的差的平方和。
样本方差的计算公式是其核心概念,它涉及样本数据与平均值的偏差平方和的处理。具体来说,样本方差(S)的计算公式为:S=√[∑(Xi-X) / (n-1)],其中Xi是每个观测值,X是样本平均值,∑表示求和,n是样本总数。
样本方差公式:E(S^2)=DX。先求出总体各单位变量值与其算术平均数的离差的平方,然后再对此变量取平均数,就叫做样本方差。样本方差用来表示一列数的变异程度。样本均值又叫样本均数。即为样本的均值。在许多实际情况下,人口的真实差异事先是不知道的,必须以某种方式计算。
样本方差是统计学中常用的一种测量数据离散程度的方法。它是指一组数据与其平均值之间的差距的平方和的平均值。样本方差的公式如下:S^2=\frac{\sum_{i=1}^n(x_i-\bar{x})^2}{n-1} 其中,$n$表示样本大小,$x_i$表示第$i$个数据,$\bar{x}$表示样本的平均值。
假设是一个样本,则样本方差的计算公式为:S^2=frac{sum_{i=1}^N(X_i-bar{X})^2}{N-1} 其中是样本均值。例如,一样本取值为3,4,4,5,4,则样本均值=bar{X}, 样本方差=S2=((3 ? 4)2 + (4 ? 4)2 + (4 ? 4)2 + (5 ? 4)2 + (4 ? 4)2)/(5-1)=0.5。
样本方差是用来衡量数据集的离散程度的统计量。它是指每个数据点与数据集均值之差的平方的平均值。样本方差可以用来评估数据的波动性或者分散程度,数值越大表示数据的离散程度越大,数值越小表示数据的离散程度越小。
样本方差公式?
样本方差公式为:S = 样本方差是衡量样本数据离散程度的一个重要指标。其计算公式如下: 公式表达:样本方差公式中的S代表样本方差,n为样本数量,X为样本数据,均值是样本数据的平均值。表示求和,即计算所有样本点与均值的差的平方和。
样本方差的公式是:S = * Σ^2 / n。其中,S代表样本方差,n是样本数量,μ是样本均值,X是样本中的各个观测值,Σ表示求和。该公式用于计算一个样本数据集中各数值与其均值之间的离散程度。
样本方差公式:E(S^2)=DX。先求出总体各单位变量值与其算术平均数的离差的平方,然后再对此变量取平均数,就叫做样本方差。样本方差用来表示一列数的变异程度。样本均值又叫样本均数。即为样本的均值。在许多实际情况下,人口的真实差异事先是不知道的,必须以某种方式计算。