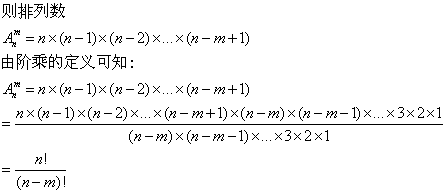plc编程循环
1、初始给一个整数地址送入0,每按一次按钮整数加1,所以整数等于1就输出灯亮,等于2就串一个SM0.5(1s周期脉冲)输出闪烁,等于3就没有输出,再按等于4时候又把1送入整数灯亮,循环这样。用按钮控制一个寄存器自加。
2、plc用计数器循环5次的方法是红绿灯控制问题一条十字路口,按一下按钮SB1南北向的绿灯就亮起,东西向的红灯亮起。按第二下按钮SB1南北向的红灯就亮起,东西向的绿灯灯亮起。按第三次按钮SB1回到第一步,红绿灯控制问题一条十字路口,按一下按钮SB1南北向的绿灯就亮起,东西向的红灯亮起。
3、PLC 的程序是自动循环的。PLC的工作过程是循环扫描的过程,循环扫描时间的长短取决于指令执行速度、用户程序的长度等因素。输出对输入的影响有滞后现象。
阶乘的计算公式
1、阶乘的计算公式是:n!=n×(n-1)×(n-2)×...×1。
2、阶乘的主要公式:任何大于1的自然数n阶乘表示方法:n!=1×2×3×?×n 或 n!=n×(n-1)!n的双阶乘:当n为奇数时表示不大于n的所有奇数的乘积 。当n为偶数时表示不大于n的所有偶数的乘积(除0外),如:8!=2×4×6×8。
3、阶乘的主要公式:任何大于1的自然数n阶乘表示方法:n!=1×2×3×……×n 或 n!=n×(n-1)!n的双阶乘:当n为奇数时表示不大于n的所有奇数的乘积 。
4、阶乘是一个自然数 n 乘以所有小于它的自然数的乘积,通常用符号 n! 表示。
5、阶乘的主要公式:任何大于1的自然数n阶乘表示方法:n!=1×2×3×……×n。n的双阶乘:当n为奇数时表示不大于n的所有奇数的乘积 ,如:7!=1×3×5×7。当n为偶数时表示不大于n的所有偶数的乘积(除0外),如:8!=2×4×6×8。
6、阶乘的公式是:n!=n*(n-1)!。它们的规律符合公式:abcd=a*a!+b*b!+c*c!+d*d!。即:该数据的值等于各个位上数字乘以其阶乘数之和。因为0-9的数字的阶乘值不会特别大,所以阶乘数也有上限。用穷举法可以找到所有的阶乘数,利用计算机求阶乘数非常的方便。
阶乘公式
1、阶乘的计算公式是:n!=n×(n-1)×(n-2)×...×1。
2、阶乘的主要公式:任何大于1的自然数n阶乘表示方法:n!=1×2×3×?×n 或 n!=n×(n-1)!n的双阶乘:当n为奇数时表示不大于n的所有奇数的乘积 。当n为偶数时表示不大于n的所有偶数的乘积(除0外),如:8!=2×4×6×8。
3、阶乘的主要公式:任何大于1的自然数n阶乘表示方法:n!=1×2×3×……×n 或 n!=n×(n-1)!n的双阶乘:当n为奇数时表示不大于n的所有奇数的乘积 。
4、阶乘是一个自然数 n 乘以所有小于它的自然数的乘积,通常用符号 n! 表示。
5、阶乘的主要公式:任何大于1的自然数n阶乘表示方法:n!=1×2×3×……×n。n的双阶乘:当n为奇数时表示不大于n的所有奇数的乘积 ,如:7!=1×3×5×7。当n为偶数时表示不大于n的所有偶数的乘积(除0外),如:8!=2×4×6×8。
6、阶乘的求和公式是:1!+2!+3!+……+N!阶乘定义:n!=n*(n-1)*(n-2)*……*1 计算方法:正整数阶乘指从 1 乘以 2 乘以 3 乘以 4 一直乘到所要求的数。例如所要求的数是 4,则阶乘式是 1×2×3×4,得到的积是 24,24 就是 4 的阶乘。
数学中!怎么计算
数学中!是阶乘的意思。n!=1×2×3×...×n。阶乘是基斯顿·卡曼(Christian Kramp,1760~1826)于 1808 年发明的运算符号,是数学术语。一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,并且0的阶乘为1。自然数n的阶乘写作n!。1808年,基斯顿·卡曼引进这个表示法。
在数学中,!代表阶乘,它是一个特定的运算符,用于计算一个正整数和所有小于它的正整数的乘积。具体来说,n的阶乘,表示为n!,是从1乘到n的所有正整数的乘积。例如,5的阶乘是1乘以2乘以3乘以4乘以5,结果是120。阶乘在数学和统计学中有广泛的应用。
在计算机运算中,运算符号! 表示布尔非 :如果 x 为 True,返回 False 。如果 x 为 False,它返回 True。在数学计算中,运算符号!表示阶乘:n!=1×2×3×...×n。一个正整数的阶乘(英语:factorial)是所有小于及等于该数的正整数的积,并且有0的阶乘为1,自然数n的阶乘写作n!。
中,首先计算4的平方,然后计算2的阶乘,但由于这里的阶乘并不直接作用于乘方的结果,而是作用于紧随其后的数字,因此这个表达式的实际含义可能有些混淆。更准确的表达应该是先明确运算顺序,或者使用括号来避免歧义。
其计算公式为Cnm = n!/m!(n-m)!,即先将n个元素全排列,再将其中任意选取的m个元素看作是同排列,因此要除以m!;同时,由于选取的元素可以是任意的m个,因此要除以(n-m)!。