微积分入门基本公式是什么?
1、微积分基本公式:第一基本定理 第二基本定理 对微积分基本定理比较直观的理解是:把函数在一段区间的“无穷小变化”全部“加起来”,会等于该函数的净变化,这里“无穷小变化”就是微分,“加起来”就是积分,净变化就是该函数在区间两端点的差。
2、微积分的基本公式共有四大公式:牛顿-莱布尼茨公式,又称为微积分基本公式;格林公式,把封闭的曲线积分化为区域内的二重积分,它是平面向量场散度的二重积分;高斯公式,把曲面积分化为区域内的三重积分,它是平面向量场散度的三重积分;斯托克斯公式,与旋度有关。
3、微积分的基本公式包括四大公式:- 牛顿-莱布尼茨公式,又称微积分基本公式。- 格林公式,将封闭曲线积分转换为区域内的二重积分,与平面向量场的散度有关。- 高斯公式,将曲面积分转换为区域内的三重积分,与平面向量场的散度有关。- 斯托克斯公式,与旋度有关。
最近对微积分很感兴趣,想了解了解,入个门,帮帮忙吧。
要学好数学,基础一定要扎实。微积分是数学分析的一部分,与初中几何部分关系不大,但初中的代数式、函数相关知识一定要学好,高中会学到三角函数、指数函数、对数函数等许多新函数,微积分与函数息息相关,这部分一定要学得很精,另外要有比较强的代数运算能力。
财会电算化,可能不学高数,但是高数的主体之一:微积分是肯定要学的。电子技术与计算机应用、计算机应用与网络技术、电子信息工程技术 是肯定要学高数的 公共关系学、职业素质教育 很大可能要学,毕竟高数是大学的基础课。
十八世纪以来,以解析几何与微积分这两个有力工具的创立为契机,数学以空前的规模迅猛发展,出现了无数分支。由于自然界的客观规律大多是以微分方程的形式表现的,所以微分方程的研究一开始就受到很大的重视。 微分几何基本上与微积分同时诞生,高斯与黎曼的工作又产生了现代的微分几何。
内容没有区别。大学的高数学习的内容全部是微分和积分的知识。
我的一个弟兄在高数课上老师问:“微积分是很有用的学科,学习微积分,我们的目标是什么?我弟兄:没有蛀牙! 上语文课老师说:其实黄鼠狼是不吃鸡的,那是科学家经过实验得出的。 曾经把一只鸡和黄鼠狼关在一起,第二天你们猜怎么了? 同学接道:鸡怀孕了。
既然选择了考研,所以你所选择的专业甚至该专业的方向都是你所感兴趣的,因为近3年的时间要跟你所选择的专业打交道,没有兴趣的话,简直是在折磨自己,而且还浪费青春和金钱。
微积分入门什么书籍好?
推荐以下三本微积分书籍:《简明微积分》,作者:司胜。内容介绍:是普通高等教育“十五”国家级规划教材,是在第三版的基础上,根据作者近年来的教学经验及教学信息反馈修订而成。《托马斯微积分》,作者:芬尼韦尔。
《微积分原理》(PrinciplesofCalculus)-RichardCourantandRichardRobbins:这本书是另一本经典的微积分教材,以其严密的逻辑和清晰的解释而闻名。它从直观的角度出发,逐步引入导数和积分的概念,并通过大量的例题和习题帮助读者掌握微积分的技巧。
《Calculus by James Stewart》(第八版)是全球销量最高的微积分教材,以其卓越的习题和严谨的论述而闻名。被誉为“清晰、准确、充满相关实际案例的世界级教材”。 《Thomas Calculus by George B. Thomas》(第十四版)以其生动且精确的习题实例赢得了无数赞誉。
三本经典微积分教材推荐如下:《Calculus》作者James Stewart,最新版本为8e,全球销量最高,以高质习题和严谨文风闻名。作者Stewart在教育界成就卓著,也是知名的小提琴家。书内提供了大量真实世界案例,深受学习者欢迎。《Thomas Calculus》作者George B Thomas,最新版本为14e。
微积分入门(基础知识及应用)
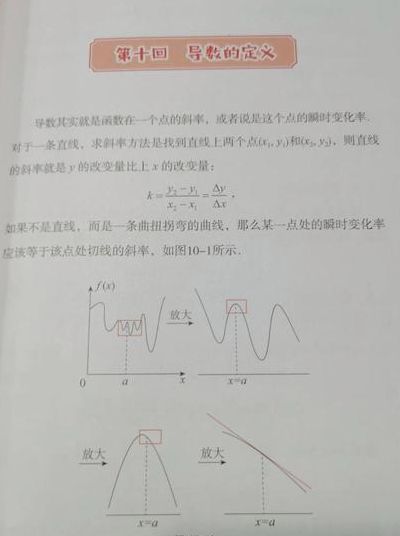
导数是微积分中最基本的概念之一,它表示函数在某一点处的变化率。导数的定义式为:f(x)=\lim\limits_{\Deltax\to0}\frac{f(x+\Deltax)-f(x)}{\Deltax} 其中,$f(x)$是函数,$f(x)$表示函数$f(x)$在$x$处的导数。
牛顿-莱布尼茨公式,又称为微积分基本公式;格林公式,把封闭的曲线积分化为区域内的二重积分,它是平面向量场散度的二重积分;高斯公式,把曲面积分化为区域内的三重积分,它是平面向量场散度的三重积分;斯托克斯公式,与旋度有关。
零基础微积分入门基本教程:微积分的基本概念和内容包括微分学和积分学。微分学的主要内容包括:极限理论、导数、微分等。积分学的主要内容包括:定积分、不定积分等。
微积分基本公式:第一基本定理 第二基本定理 对微积分基本定理比较直观的理解是:把函数在一段区间的“无穷小变化”全部“加起来”,会等于该函数的净变化,这里“无穷小变化”就是微分,“加起来”就是积分,净变化就是该函数在区间两端点的差。
微积分入门基础知识包括微分学和积分学。微分学的主要内容包括极限理论、导数、微分等。积分学的主要内容包括定积分、不定积分等。从广义上说,数学分析包括微积分、函数论等许多分支学科,但是现在一般已习惯于把数学分析和微积分等同起来,数学分析成了微积分的同义词,一提数学分析就知道是指微积分。
微积分的基本公式共有四大公式牛顿-莱布尼茨公式,又称为微积分基本公式;格林公式,把封闭的曲线积分化为区域内的二重积分,它是平面向量场散度的二重积分;高斯公式,把曲面积分化为区域内的三重积分,它是平面向量场散度的三重积分;斯托克斯公式,与旋度有关。
微积分入门基本公式
常数倍积分公式:∫ kdx = kx + C 其中,k 是任意常数。 幂函数积分公式:∫ x^μ dx = μx^(μ+1)/(μ+1) + C 注意:当 μ ≠ -1 时适用。
个基本的微积分公式如下: 对于常数C,其微分为0,即 d(C) = 0。 对于x的μ次方,其微分为μx^(μ-1)dx。 对于ax,其微分为axln(a)dx。 对于ex,其微分为exdx。 对于a的x次方,其微分为1/(xln(a))dx。 对于ln(x),其微分为1/xdx。
基本积分表共24个公式:∫ kdx = kx + C (k是常数 ) x μ ∫ x dx = μ + 1 + C , ( μ ≠ ?1) μ +1dx ( 3) ∫ = ln | x | + C x1 ( 4) ∫ dx = arctan x + C 2 1+ x 1 。
微积分基本公式:第一基本定理 第二基本定理 对微积分基本定理比较直观的理解是:把函数在一段区间的“无穷小变化”全部“加起来”,会等于该函数的净变化,这里“无穷小变化”就是微分,“加起来”就是积分,净变化就是该函数在区间两端点的差。
微积分的基本公式共有四大公式:牛顿-莱布尼茨公式,又称为微积分基本公式;格林公式,把封闭的曲线积分化为区域内的二重积分,它是平面向量场散度的二重积分;高斯公式,把曲面积分化为区域内的三重积分,它是平面向量场散度的三重积分;斯托克斯公式,与旋度有关。
零基础微积分入门基本教程
零基础微积分入门基本教程:微积分的基本概念和内容包括微分学和积分学。微分学的主要内容包括:极限理论、导数、微分等。积分学的主要内容包括:定积分、不定积分等。
间断点的分类首先,让我们通过实例理解可去间断点。例如,考虑函数 看似简单,但当在 0 处函数值被零分母限制,导致传统定义下无法确定该点的函数值。直观上,函数图像在 0 处断裂。然而,如果我们人为地将函数值设为 lim(x-0) f(x),这个点就可“去”除,使函数连续起来。
本教程旨在为独立学院的理、工、经、管、医等专业学生提供全面的微积分基础知识。首先,我们从基础出发,探讨 第一章:函数 1 函数的概念:我们将介绍函数的基本定义,帮助理解其在数学中的核心地位。2 由已知函数产生的新函数:学习如何通过已知函数构建新函数,掌握函数的组合技巧。
Zorich的Mathematical Analysis(2nd edition): 俄式著作,内容详尽,讲解细致,习题质量高,但不适合入门。 菲赫金哥尔茨的微积分学教程(第8版): 包含微积分应用,内容详实,但篇幅过大,篇幅过大,可能更适合查阅。推荐书籍的电子版与翻译版本已整理并提供下载链接。
首先,建议你从基础知识开始学习。了解微积分的基本概念和术语,例如极限、导数、积分等。可以通过阅读教科书、参加在线课程或观看教学视频来获得这些知识。其次,注重理解而不仅仅是记忆。微积分是一门抽象的数学学科,理解和应用概念比简单地记住公式更为重要。
- 二重积分的计算:掌握积分计算方法。- 二重积分的应用:解决实际问题中的多变量积分问题。- MATLAB计算二重积分:实际操作MATLAB解决二重积分问题。第七章:常微分方程及差分方程 - 微分方程的基本概念:定义和分类。- 常见的一阶微分方程:解决和理解基本微分方程。