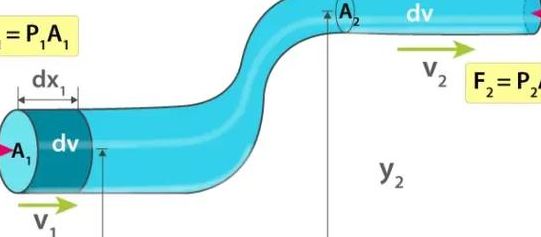
有截止的伯努利公式
有截止的伯努利公式:(1+x)^n1+nx (x0,n=2)。伯努利定律:在一个流体系统,比如气流、水流中,流速越快,流体产生的压力就越小。p+ρgz+(1/2)*ρv^2=C,式中p、ρ、v分别为流体的压强、密度和速度;z 为铅垂高度;g为重力加速度。
p+1/2ρv2+ρgh=C。伯努利原理往往被表述为p+1/2ρv2+ρgh=C,这个式子被称为伯努利方程。式中p为流体中某点的压强,v为流体该点的流速,ρ为流体密度,g为重力加速度,h为该点所在高度,C是一个常量。它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。
i.e.P1+h1ρg+1/2ρv^2=C。
流体的伯努利定理
1、流体在管道中流动时,管道中的压力与流量的关系可以用伯努利定理来描述。伯努利定理表明,在一个无摩擦的流场中,流体的速度增加,则其压强降低;反之,流体的速度减小,则其压强增加。
2、流体的伯努利定理:在一个流体系统,比如气流、水流中,流速越快,流体产生的压强就越小,这就是被称为“流体力学之父”的丹尼尔·伯努利1738年发现的“伯努利定理”。
3、流体的伯努利定理适用于:任何流体,包括气体和液体。伯努利方程的适用条件是流体流动必须是恒定流,而且是不可压缩流体,作用在流体上的质量力只有重力,建立能量方程的两个过水断面都必须位于均匀流或渐变流段。简介 丹尼尔·伯努利在1726年提出了“伯努利原理”。
4、伯努利定理的数学公式为:P + 1/2ρv^2 + ρgh = 常数。其中,P代表流体的压力,ρ表示流体的密度,v是流体的速度,g为重力加速度,h则是流体的高度。这个公式清晰地展示了,在不可压缩流体中,流速增加时,压力降低,但整体能量保持不变。伯努利定理的应用范围非常广泛。
5、伯努利定理是流体力学中最基本的定理之一,它描述了在不可压缩流体中速度增加时压力降低的现象。该定理由瑞士数学家丹尼尔·伯努利在1738年提出,被广泛应用于气体、液体、风力机、飞行器等领域。伯努利定理的表达式为:P+1/2ρv^2+ρgh=常数,其中P为压力,ρ为密度,v为速度,h为高度。
伯努利定律的公式是什么?
p+1/2ρv2+ρgh=C。伯努利原理往往被表述为p+1/2ρv2+ρgh=C,这个式子被称为伯努利方程。式中p为流体中某点的压强,v为流体该点的流速,ρ为流体密度,g为重力加速度,h为该点所在高度,C是一个常量。它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。
伯努利定理的数学公式为:P + 1/2ρv^2 + ρgh = 常数。其中,P代表流体的压力,ρ表示流体的密度,v是流体的速度,g为重力加速度,h则是流体的高度。这个公式清晰地展示了,在不可压缩流体中,流速增加时,压力降低,但整体能量保持不变。伯努利定理的应用范围非常广泛。
伯努利方程的公式是p+1/2ρv2+ρgh=C 伯努力的定律是在一个流体系统,比如气流、水流中,流速越快,流体产生的压强就越小,这就是被称为“流体力学之父”的丹尼尔·伯努利1738年发现的“伯努利定理”。
对于不可压缩的流体,伯努利定理可以表示为:p + ρgz + ρv^2/2 = 常数 其中,p为流体压强,ρ为流体密度,g为重力加速度,z为流体所在的高度,v为流体速度。在管道中,流体的速度与其流量有关。
流体力学伯努利的方程是p+1/2ρv2+ρgh=C。p为流体中某点的压强,v为流体该点的流速,ρ为流体密度,g为重力加速度,h为该点所在高度,C是一个常量。它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。
在一个流体系统(如气流、水流)中,流速越快,流体产生的压力就越小,这就是“伯努利定律”。这个压力产生的力量是巨大的,空气能够托起沉重的飞机,就是利用了伯努利定律。