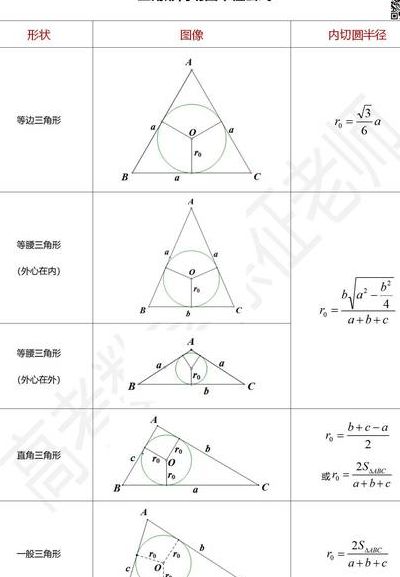
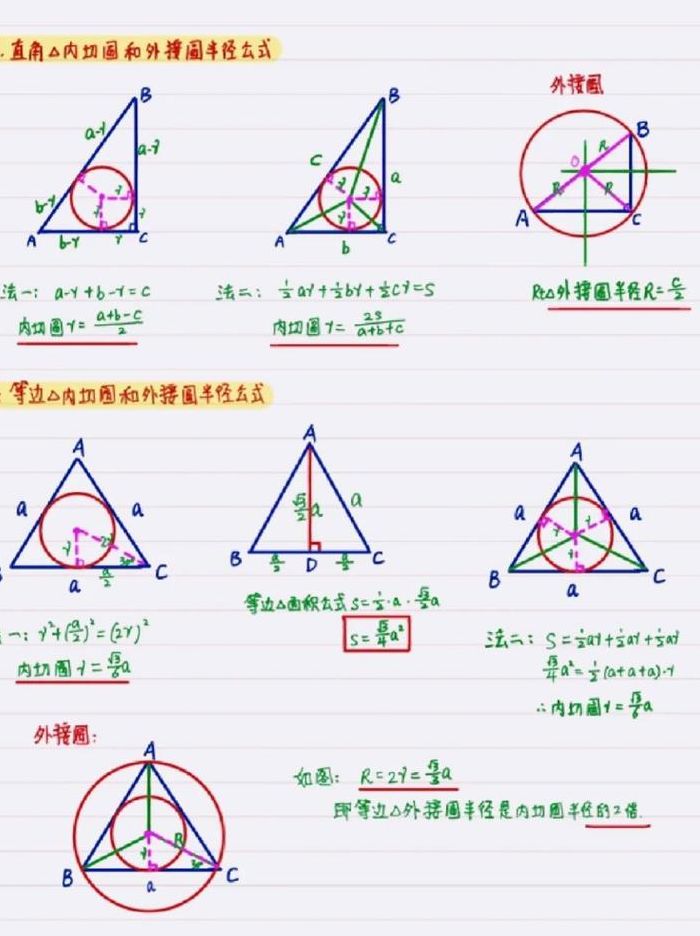
三角形内切圆的半径怎么算呢?
在直角三角形的内切圆中,有这样两个简便公式:两直角边相加的和减去斜边后除以2,得数是内切圆的半径。即:r=(a+b-c)/2 两直角边乘积除以直角三角形周长,得数是内切圆的半径。
设已知一边和它的对角,那么它的外接圆的半径R:R=a/2sinA;R=b/2sinB;R=c/2sinC;其中,A、B、C表示三角形的三个角,a、b、c分别表示三个角对应的变。
三角形内切圆和外切圆半径计算方法:三角形内切圆半径:r=2s/(a+b+c)。式中s是三角形的面积,(a+b+c)是三角形的周长。三角形外接圆的半径:R=abc/4s公式中a,b,c分别为三角形的三边,S为面积。
直角三角形的内切圆半径r=(a+b-c)/2,其中a、b是直角边长,c是斜边长 一般三角形:r=2S/(a+b+c),其中S是三角形面积,a、b、c是三角形三边。
设△ABC的三边分别为a、b、c,面积为S,内切圆半径为r,则:1/2ar+1/2br+1/2cr=S ∴r=2S/(a+b+c)这就是三角形中内切圆半径的计算公式,即三角形中内切圆半径等于面积的2倍除以周长。在三角形中,三个角的角平分线的交点是内切圆的圆心,圆心到三角形各个边的垂线段相等。
三角形内切圆半径公式:r=2S/(a+b+c)。推导:设内切圆半径为r,圆心O,连接OA、OB、OC,得到三个三角形OAB、OBC、OAC。那么,这三个三角形的边AB、BC、AC上的高均为内切圆半径r。
三角形内切圆半径、外切圆半径怎么计算?
1、三角形内切圆半径:r=2s/(a+b+c)。式中s是三角形的面积,(a+b+c)是三角形的周长。三角形外接圆的半径:R=abc/4s公式中a,b,c分别为三角形的三边,S为面积。与三角形三边都相切的圆叫做三角形的内切圆,圆心叫做三角形的内心,三角形叫做圆的外切三角形。
2、直角三角形的内切圆半径和外接圆半径可以利用其边长直接计算。内切圆半径的公式为r=(a+b-c)/2,其中a和b是直角三角形的两个直角边,c是斜边。外接圆半径的公式为R=C/2,C同样表示斜边的长度。为了证明内切圆半径的公式,可以利用三角形面积的计算方法。
3、三角形内切圆半径:r=2S/(a+b+c);三角形外接圆的半径:R=abc/4S。其中,S为三角形的面积,a,b,c分别为三角形的三边。三角形的内切圆圆心定在三角形内部,三个角的角平分线的交点是内切圆的圆心,圆心到三角形各个边的垂线段相等。
4、三角形外接圆半径R=a除以2sinA=b除以2sinB=C除以2sinc 内切圆半径r=2S除以(a+b+c) ,S是三角形面积。 直角三角形的形外接圆半径=斜边一半、内切圆半径=直角边的和减斜边后的一半。
5、内切圆半径公式 内切圆半径 r = P = / 2,其中a、b为直角三角形的直角边,c为斜边。解释:直角三角形的内切圆半径与三角形的边长有关。这个公式是通过将直角三角形的两个直角边和斜边代入计算得出的。内切圆的圆心位于三角形的内心,与三角形的三个顶点相切。
三角形内切圆半径公式是什么?
1、三角形内切圆半径公式为:r = s × / ,其中r是半径,s是三角形的半周长,n是多边形的边数。这个公式反映了三角形内切圆半径与三角形边数及其半周长之间的关系。三角形内切圆半径的求解涉及三角形几何学中一个关键的概念——角平分线定理。
2、若三角形ABC是直角三角形,内切圆半径公式为r=(a+b-c)÷2。推导过程如下:已知三角形的面积公式:S=底长×高÷2。设AB=c;BC=a;AC=b;则:S△OAB=AB×r÷2= c×r÷2,S△0BC= BC×r÷2=a×r÷2,S△OAC= AC×r÷2= b×r÷2,S△ABC=AC×BC÷2= b×a÷2。
3、三角形内切圆半径公式为:r = s × / ,其中r是内切圆的半径,s是三角形的半周长,n是三角形的边数。详细解释如下:三角形内切圆的概念 三角形内切圆是指与三角形的三条边都相切的圆。这个圆有一个很重要的性质,即其圆心位于三角形的内部,并且与每条边都有切点。
4、三角形内切圆半径:r=2s/(a+b+c)。式中s是三角形的面积,(a+b+c)是三角形的周长。三角形外接圆的半径:R=abc/4s公式中a,b,c分别为三角形的三边,S为面积。与三角形三边都相切的圆叫做三角形的内切圆,圆心叫做三角形的内心,三角形叫做圆的外切三角形。