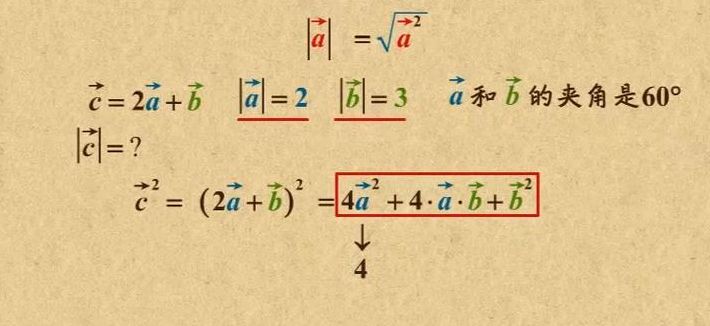向量的模怎么求（a向量加b向量的模怎么求）

向量和的模怎么求

向量和的模是|a+b|=根号下（|a|^2+|b|^2+2|a||b|cosx），向量的模的运算没有专门的法则，一般都是通过余弦定理计算两个向量的和、差的模。多个向量的合成用正交分解法，如果要求模一般需要先算出合成后的向量。模是绝对值在二维和三维空间的推广，可以认为就是向量的长度。

|a+b|=根号下（|a|^2+|b|^2+2|a||b|cosx） x为向量a、b的夹角向量的模的计算公式：空间向量模长是√x y z；平面向量模长是√xz。向量的模公式：空间向量(xyz)，其中xyz分别是三轴上的坐标，模长是：2√x2yz。平面向量(x， y)，模长是： √x y。

计算向量a和向量b的模的平方和，即a的模的平方加上b的模的平方。计算向量a和向量b的点积，并将其乘以2。用第1步计算结果减去第2步计算结果，得到向量a和向量b的和的模的平方。将第3步计算结果开方，得到向量a和向量b的和的模的值。

向量的模的求法如下：利用向量的数量积运算和性质求模。利用分类讨论思想求模。利用数形结合思想求模。利用方程思想求模。利用向量的坐标运算求模。求向量的模公式：f＝ok＊f。在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小和方向的量。

向量的模是有向线段AB的长度叫做向量的模。向量的模是指这个线段的长度，设向量a=x，y，则向量a的模=根号x方+y方，即长度，a向量加b向量等于把a向量，b向量移到同一起点，作平行四边形或三角形法则的起点的那条对角线，其长即为，a向量加b向量的模。

定义法：根据向量的模的定义，向量的模等于向量的大小，即向量的长度或范数。对于一个向量a，其模记作|a|，定义为：|a|=√a。勾股定理：对于一个二维向量a=（x，y），可以通过勾股定理求出其模长。

向量的模可以通过向量的坐标来计算。对于一个二维向量A(a1，a2)，它的模可以按照以下公式计算：|A|=√(a1+a2)。向量：在数学中，向量（也称为欧几里得向量、几何向量），指具有大小（magnitude）和方向的量。它可以形象化地表示为带箭头的线段。

|(a，b)| = 根号下(a2+b2)这个公式适用于二维向量。

设a=(x，y)，则|a|=√[x2＋y2]。向量是数学、物理学和工程科学等多个自然科学中的基本概念，指一个同时具有大小和方向，且满足平行四边形法则的几何对象。在物理学和工程学中，几何向量更常被称为矢量。许多物理量都是矢量，比如一个物体的位移，球撞向墙而对其施加的力等等。

向量的模的计算方法如下：假设向量表示为a = ，那么该向量的模计算公式为：向量模 = 。其中，x和y为向量的坐标值。简而言之，向量的模就是对向量长度的一个量化表示。具体到计算过程，需要将向量的坐标值代入公式进行计算即可得出结果。

1、求向量的模公式：f=ok*f。在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小和方向的量。它可以形象化地表示为带箭头的线段。矢量是一种既有大小又有方向的量，又称为向量。一般来说，在物理学中称作矢量，例如速度、加速度、力等等就是这样的量。

2、求向量的模的方法：定义法：根据向量的模的定义，向量的模等于向量的大小，即向量的长度或范数。对于一个向量a，其模记作|a|，定义为：|a|=√a。勾股定理：对于一个二维向量a=（x，y），可以通过勾股定理求出其模长。

3、向量的模是有向线段AB的长度叫做向量的模。向量的模是指这个线段的长度，设向量a=x，y，则向量a的模=根号x方+y方，即长度，a向量加b向量等于把a向量，b向量移到同一起点，作平行四边形或三角形法则的起点的那条对角线，其长即为，a向量加b向量的模。

1、向量的模的求法如下：利用向量的数量积运算和性质求模利用分类讨论思想求模利用数形结合思想求模利用方程思想求模利用向量的坐标运算求模求向量的模公式：f=ok*f。在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小和方向的量。

2、向量的模也被称为向量的长度或向量的大小。对于一个二维向量（x，y）或三维向量（x，y，z），可以使用以下公式来计算向量的模：|v|=√（x^2+y^2）（二维向量），|v|=√（x^2+y^2+z^2）（三维向量）。表示乘方运算是^，表示平方根运算是√。

3、定义法：根据向量的模的定义，向量的模等于向量的大小，即向量的长度或范数。对于一个向量a，其模记作|a|，定义为：|a|=√a。勾股定理：对于一个二维向量a=（x，y），可以通过勾股定理求出其模长。

向量的模的求法如下：利用向量的数量积运算和性质求模利用分类讨论思想求模利用数形结合思想求模利用方程思想求模利用向量的坐标运算求模求向量的模公式：f=ok*f。在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小和方向的量。