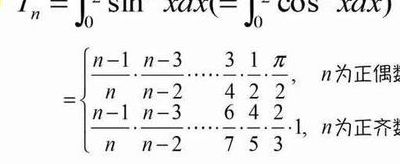张宇点火公式
1、点火公式一般指Wallis公式,Wallis(华里士)公式是关于圆周率的无穷乘积的公式,但Wallis公式中只有乘除运算,连开方都不需要,形式上十分简单。虽然Wallis公式对π的近似计算没有直接影响,但是在导出Stirling公式中起到了重要作用。
2、(3/4)×(1/2)×(π/2) 华里士公式,张宇所说的点火公式。答案是(3π/16)。
3、点火公式,源于Wallis公式在考研数学中的应用,张宇老师生动的表述,揭示了正弦与余弦之间的奇妙联系。Wallis公式,作为数学历史上的一个重要成果,不仅在数论领域展现其独特魅力,也在数学分析中扮演着重要角色。在考研数学中,Wallis公式帮助解决了一系列复杂的积分问题。
∫cos^4xdx的答案是什么?
1、(3/4)×(1/2)×(π/2) 华里士公式,张宇所说的点火公式。答案是(3π/16)。
2、∫cos^4xdx=1/32sin4x+1/4sin2x+3/8x+C。(C为积分常数)连续使用高中公式cos2x=2cos^2x-1达到降幂效果。
3、对他积分得:1/32*sin4x-1/4*sin2x+x/8 由于α不好打,用x代替了,其实就是两次半角公式,相信你一定知道的,就是没想到。多做题就好了。
点火公式(Wallis公式)在考研数学中的应用,及Wallis推导
将Wallis公式应用于正弦和余弦,我们发现两者似乎遵循相同的规律。这背后的秘密在于数学中的对称性与一致性。通过简单的换元操作,我们可以将正弦转换为余弦,反之亦然,从而证明了两者点火公式的一致性。这一过程不仅展示了数学的逻辑美感,也为考研数学中处理这类问题提供了实用的方法。
考研数学中,Wallis公式(也被称为华里士公式或沃利斯公式)以其独特的方式被提及,特别是在点火公式这个概念中。具体来说,Wallis公式涉及到正弦和余弦函数的计算,它在处理相关问题时显得尤为关键。尽管公式推导本身在这篇文章中并未详述,但可以提供两个链接供有兴趣的同学深入了解。
Wallis(华里士)公式,即点火公式,是关于圆周率的无穷乘积的公式。这个公式在形式上十分简单,因为它只有乘除运算,甚至不需要开方。尽管Wallis公式对π的近似计算没有直接影响,但它在导出Stirling公式中起到了关键作用。在三角函数的积分中,点火公式非常常用,也是考研数学中常见的考点。
华里氏公式,亦被宇哥视为考研必考之一,其复杂多变,但并非无迹可循。总结而言,此公式在实际应用中通常涉及以下几种基本形式。首先,当n为偶数时,公式表现为一种特定的数学运算。例如:当n为偶数时,公式=特定运算表达式 接者,当n为奇数时,公式则会呈现另一种模式。
点火公式一般指Wallis公式,Wallis(华里士)公式是关于圆周率的无穷乘积的公式,但Wallis公式中只有乘除运算,连开方都不需要,形式上十分简单。虽然Wallis公式对π的近似计算没有直接影响,但是在导出Stirling公式中起到了重要作用。点火公式在三角函数的积分里非常常用,也是考研最爱考的一个数学公式。
考研数一听谁的课
在选择考研数一课程时,推荐几位老师各有特色。张宇的授课风格幽默风趣,高数讲授得深入浅出,适合强化阶段学习。不过,对于基础较为薄弱的考生来说,张宇的课程可能略显吃力。汤家凤则是一位十分实在的老师,他的高数课程同样受到了广泛的好评。汤老师的教学内容扎实,适合基础段学习。
考研数学数一课程选择上,张宇、汤家凤、李永乐和王式安都是值得考虑的老师。张宇的授课风格幽默风趣,高数讲授尤为出色,但可能不太适合初学者,更适合强化阶段的学生。汤家凤则以其诚信和负责的态度著称,高数讲授同样优秀,适合基础阶段的学生。
考研数学一的基础学习至关重要,选择一位基础扎实的老师可以为后续的学习奠定坚实的基础。对于数学基础的学习,建议选择来自著名高校的数学系教授或是有丰富授课经验的培训机构教师。因为数学作为一门基础学科,扎实的基础是掌握和应用高深数学知识的前提。听数学基础扎实的老师讲授课程,可以增加学习的保障性。
张宇,人称宇哥,我复习高数时的主要导师。他的课程风趣幽默,擅长将抽象数学问题形象化,让原本枯燥乏味的数学变得生动有趣。上课没有压力,轻松愉快。如果你对数学不甚感兴趣,认真听宇哥的课,结合复习全书做一遍,效果显著。听课时,务必打印出他的讲义,这样效果更佳,更有针对性。
高数问题,详细如图?
1、求极限的时候,只有在积分项相乘并且其极限值为常数的时候才可以代入并提出去。你的第二个表达式,因为它是和式,所以只是分别在求极限而已,不能 直接带成1。详细如图所示:高数求极限方法:01 定义法。
2、如图高数问题,判断级数敛散性过程见上图。此高数问题,判断敛散性,可以将一般项与1/n的极限等于常数1/4,而级数1/n收敛,所以,原级数收敛。这用高数的一个判断级数敛散的定理。具体的判断如图问题的敛散性的详细步骤及说明见上。
3、②2(2)收敛 这个题目主要是数列的形式比较复杂,因此需要写出来重新整理。如图:写成这种形式之后,观察到这个是一个交错级数,且每一项绝对值单调递减,由莱布尼茨判别法,这个级数收敛。