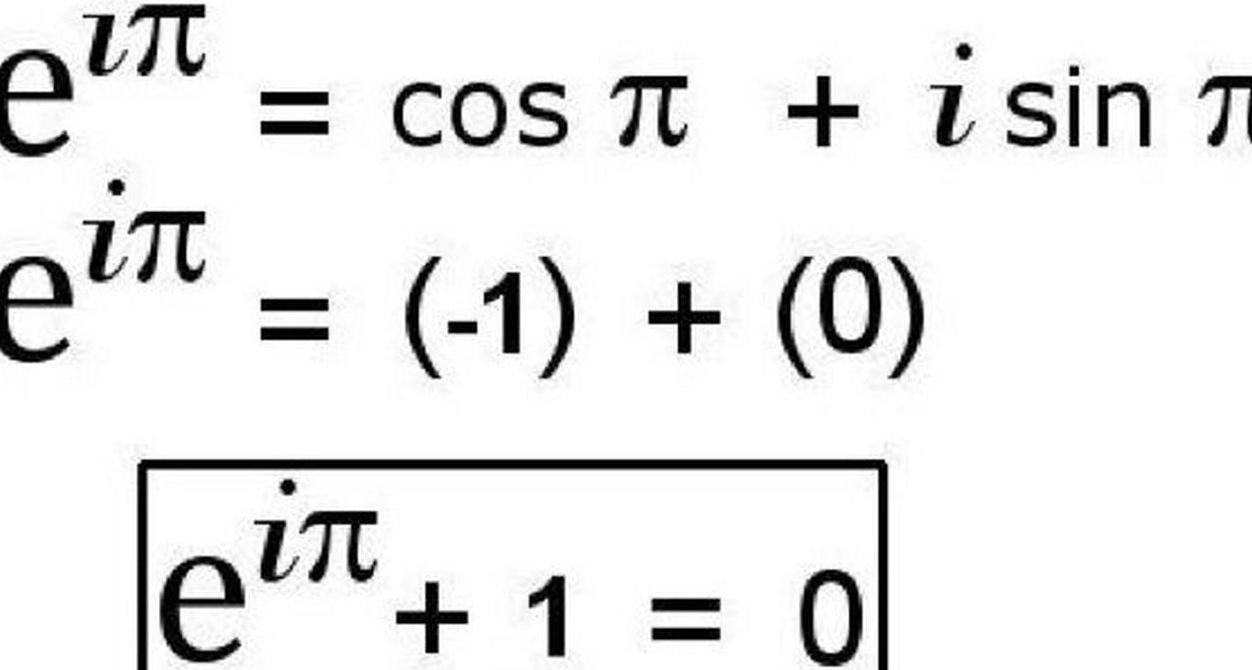欧拉定理的公式是什么?
欧拉公式的三种形式如下:R+V-E=2,在任何一个规则球面地图上,用R记区域个数,V记顶点个数,E记边界个数,则R+V-E=2,这就是欧拉定理。此定理由Descartes首先给出证明,后来Euler独立给出证明,欧拉定理亦被称为欧拉公式。
欧拉公式的三种形式如下:R+V-E=2,在任何一个规则球面地图上,用R记区域个数,V记顶点个数,E记边界个数,则R+V-E=2,这就是欧拉定理,它于1640年由Descartes首先给出证明,后来Euler于1752年又独立地给出证明,我们称其为欧拉定理,在国外也有人称其为Descartes定理。
欧拉定理公式是:V+F-E=2。简单多面体的顶点数V、面数F及棱数E间有关系,公式描述了简单多面体顶点数、面数、棱数特有的规律。欧拉在1750年独立地发现了这个公式,并于1752年发表。
欧拉定理公式是e^(iπ)+1=0。欧拉公式 欧拉公式在不同的学科中有着不同的含义。复变函数中,e^(ix)=(cosx+isinx)称为欧拉公式,e是自然对数的底,i是虚数单位。
欧拉定律是数学中的一组定理,由瑞士数学家欧拉提出。它包括欧拉公式、欧拉恒等式和欧拉积分公式等。 欧拉公式:e^(iπ) + 1 = 0。这个公式将自然对数的底e、虚数单位i、圆周率π和复数的单位1统一在一起。 欧拉恒等式:e^(ix) = cosx + isinx,其中x为实数。
欧拉公式的表达式是什么?
欧拉公式表达为:e^(ix) = cos(x) + i*sin(x)。在这个公式中,e代表自然对数的底数,i是虚数单位。该公式将三角函数的定义域扩展到了复数领域,并建立了三角函数与指数函数之间的联系,在复变函数理论中占据着极其重要的地位。
欧拉公式是数学中一条重要的等式,它将自然对数的底数e、虚数单位i、π和三角函数(正弦和余弦)联系在一起。
欧拉公式是工程力学中的一个重要公式,用于计算细长压杆的临界载荷。具体表达式为:\(P_{cr} = \frac{\pi^2 EI}{(KL)^2}\),其中,\(E\)代表材料的弹性模量,\(I\)是截面惯性矩,\(l\)为压杆长度,\(K\)为长度系数,与压杆的支承情况有关,而\(\mu\)是约束系数。
欧拉公式是一种描述复数指数运算的公式,由瑞士数学家欧拉于18世纪发现。它表达式为e^(ix)=cos(x)+isin(x),其中e表示自然对数的底数,i表示虚数单位,x为实数。
欧拉公式是数学中的一个重要公式,它将三角函数与指数函数联系起来。欧拉公式的表达式为:e^(ix)=cosx+isinx,其中i是虚数单位,x是实数。首先,我们需要了解三角函数和指数函数的定义。三角函数是一类特殊的函数,它们在直角三角形中定义,包括正弦函数sin、余弦函数cos和正切函数tan。
欧拉公式是复数学说中的一个核心公式,它是由瑞士数学家莱昂哈德欧拉提出的。这个公式展示了复平面上的几何性质和实数的联系。复数通常由实数和虚数组成,而欧拉公式则展示了如何将实数通过特定的数学运算转化为复数形式。公式的具体表达 欧拉公式的核心在于它揭示了指数函数的特性。
欧拉公式是一种什么公式?
1、欧拉公式是一个在复数学说中的重要公式,它揭示了实数、虚数与复数的内在关系。欧拉公式的内容为:对于任何实数x,欧拉公式表示为e^ = cos + isin。其中,e是自然对数的底数,i是虚数单位,cos和sin分别表示余弦和正弦函数。
2、欧拉公式是一种描述复数指数运算的公式。欧拉公式是一种描述复数指数运算的公式,由瑞士数学家欧拉于18世纪发现。它表达式为e^(ix)=cos(x)+isin(x),其中e表示自然对数的底数,i表示虚数单位,x为实数。
3、欧拉公式,一个被誉为“上帝创造的公式”的数学表达式,其形式为[公式],其中e代表自然对数的底,i是虚数单位。当x取特定值[公式]时,欧拉公式可转化为[公式],这个公式涵盖了e、i、[公式]、1和0这五个基本数,其中e和[公式]为超越数,而0和1是自然数的基础。
4、欧拉公式是一条基本的数学公式,它描述了三个关键数学概念:欧拉常数、虚数单位和三角函数。数学家欧拉在18世纪末提出了该公式,并广泛应用于数学、物理、工程和计算机科学等领域。欧拉公式在数学界中被广泛使用,特别是在解决函数论、概率论、复变函数及矩阵理论等问题时起到重要的作用。
欧拉公式是什么公式?
欧拉公式是一个在复数学说中的重要公式,它揭示了实数、虚数与复数的内在关系。欧拉公式的内容为:对于任何实数x,欧拉公式表示为e^ = cos + isin。其中,e是自然对数的底数,i是虚数单位,cos和sin分别表示余弦和正弦函数。
欧拉公式三种形式分别是:分式里的欧拉公式=a^r/(a-b)(a-c)+b^r/(b-c)(b-a)+c^r/(c-a)(c-b),复变函数论里的欧拉公式为e^ix=cosx+isinx,三角形中的欧拉公式为d^2=R^2-2Rr。把复指数函数与三角函数联系起来的一个公式,e是自然对数的底,i是虚数单位。
欧拉公式表达为:e^(ix) = cos(x) + i*sin(x)。在这个公式中,e代表自然对数的底数,i是虚数单位。该公式将三角函数的定义域扩展到了复数领域,并建立了三角函数与指数函数之间的联系,在复变函数理论中占据着极其重要的地位。
欧拉公式,一个被誉为“上帝创造的公式”的数学表达式,其形式为[公式],其中e代表自然对数的底,i是虚数单位。当x取特定值[公式]时,欧拉公式可转化为[公式],这个公式涵盖了e、i、[公式]、1和0这五个基本数,其中e和[公式]为超越数,而0和1是自然数的基础。
欧拉公式是一种描述复数指数运算的公式,由瑞士数学家欧拉于18世纪发现。它表达式为e^(ix)=cos(x)+isin(x),其中e表示自然对数的底数,i表示虚数单位,x为实数。
欧拉公式是什么?
欧拉公式是一个在复数学说中的重要公式,它揭示了实数、虚数与复数的内在关系。欧拉公式的内容为:对于任何实数x,欧拉公式表示为e^ = cos + isin。其中,e是自然对数的底数,i是虚数单位,cos和sin分别表示余弦和正弦函数。
欧拉公式表达为:e^(ix) = cos(x) + i*sin(x)。在这个公式中,e代表自然对数的底数,i是虚数单位。该公式将三角函数的定义域扩展到了复数领域,并建立了三角函数与指数函数之间的联系,在复变函数理论中占据着极其重要的地位。
多面体的欧拉公式是:V+F–E=2。若用F表示一个正多面体的面数,E表示棱数,V表示顶点数,则有F+V-E=2,即“表面数+顶点数-棱长数=2”。F+V-E=2,这个公式叫欧拉公式。公式描述了简单多面体顶点数、面数、棱数特有的规律。
欧拉公式的表述为:对于任何凸多面体,顶点数V、面数F与棱长数E之间的关系满足V - E + F = 2。这里的顶点数V指的是多面体的顶点数量,面数F指的是多面体的面数量,棱长数E指的是多面体的棱长数量。公式表明,对于任何凸多面体,顶点数、面数与棱长数之间的关系总是一个常数2。
欧拉公式是:e^(ix)=cos(x)+i*sin(x)。欧拉公式在不同的学科中有着不同的含义。复变函数中,e^(ix)=(cos x+isin x)称为欧拉公式,e是自然对数的底,i是虚数单位。拓扑学中,在任何一个规则球面地图上。
欧拉公式是一种描述复数指数运算的公式,由瑞士数学家欧拉于18世纪发现。它表达式为e^(ix)=cos(x)+isin(x),其中e表示自然对数的底数,i表示虚数单位,x为实数。