菱形的判定（菱形的判定数学）

菱形的判定方法有几种?

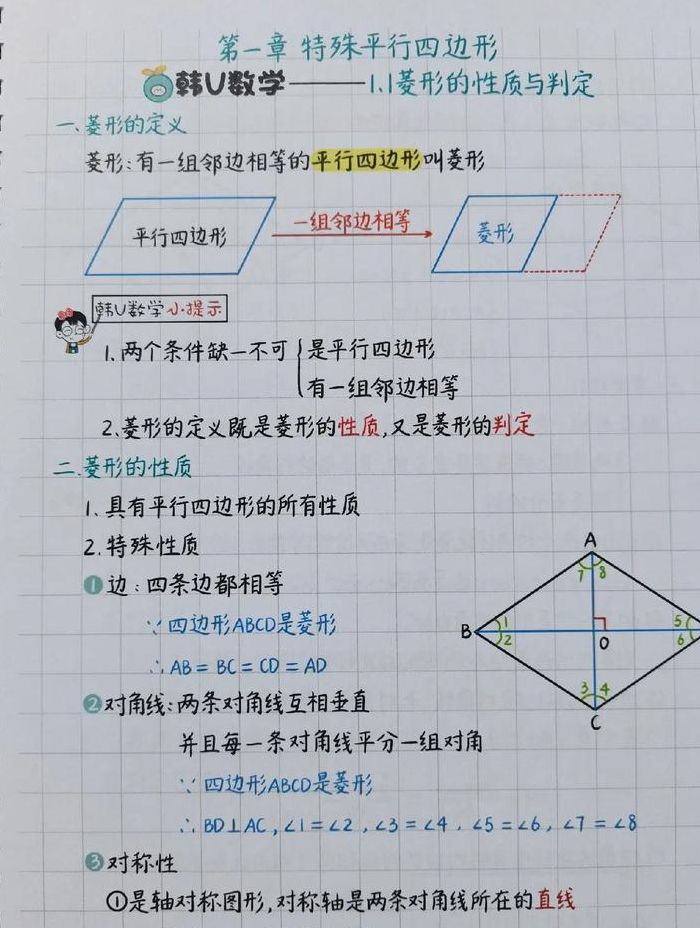
1、方法一：根据边长判定如果一个四边形的四条边全都相等，那么这个四边形就是菱形。因为所有相邻的边都相等，所以对角线互相平分，因此对角线长度也相等。此时可以用勾股定理来证明它们的长度相等，即对于菱形 ABCD，设 AC=DB=a，则有AC^2+BD^2=AD^2+BC^2=2a^2，因此AC=BD=√2a。

2、除了直接测量边长外，还可以通过计算角度来判断是否为菱形。在一个四边形中，如果相对的两角之和等于180度且所有边等长，则该四边形为菱形。这是因为相对的两角互补以及等长的边都符合菱形的几何特征。所以此判定方式是一种更为精确的识别方法。以此方式进行判断可以避免因为不完整的图形信息而导致的误判。

3、菱形的判定方法包括以下几种：一组邻边相等的平行四边形可以被认定为菱形。这意味着在一个平行四边形中，如果任意相邻的两边长度相等，那么这个平行四边形就是菱形。四边长度完全相等的四边形同样属于菱形。即四边形的四条边的长度都相同，这样的四边形即为菱形。

4、菱形的判定方法主要有以下几种：定义法根据菱形的定义，四边相等的平行四边形就是菱形。因此，只要证明一个四边形是平行四边形且四边相等，即可判定为菱形。对角线性质菱形的对角线相互垂直且平分。如果一个平行四边形中，对角线满足这两个条件，则可以判定为菱形。

5、一条对角线平分一个顶角的平行四边形是菱形有一组邻边相等的平行四边形是菱形(既可以作为定理，也可以作为判定)。对角线互相垂直的平行四边形是菱形。四边相等的四边形是菱形。4 .对角线互相垂直平分的四边形是菱形。

6、菱形的判定方法有4种。菱形的判定方法：四条边均相等。对角线互相垂直平分。两条对角线分别平分每组对角。有一对角线平分一个内角。菱形判定具体说明：次连接四边形各边中点所得的四边形称为中点四边形。不管原四边形的形状怎样改变，中点四边形的形状始终是平行四边形。

菱形的判定及定义

1、菱形判定定理：四边都相等的四边形是菱形。对角线互相垂直的平行四边形是菱形。一组邻边相等的平行四边形是菱形。

2、菱形是一种特殊的平行四边形，其显著特征在于四条边等长，但斜对角线长度不相等。因此，菱形具备独特的几何属性。定义指出，菱形的四条边必须完全相等，这是其最基本的条件之一。除了四边等长，菱形的另一个关键属性是对角线互相垂直。

3、根据菱形的定义，一组邻边相等的平行四边形是菱形。因此，可以通过测量平行四边形的四边长度，如果一组相邻边相等，则该平行四边形为菱形。性质判定菱形具有对角相等且互相垂直平分的性质。根据这一性质，可以通过测量并计算平行四边形的对角线长度及角度来判断是否为菱形。

4、菱形首先有平行四边形的性质：两条边互相平行，对边相等，对角相等，对角线互相平分，是中心对称图形此外，菱形四条边都相等，对角线互相垂直平分且平分每一组对角，既是中心对称图形又是轴对称图形，对称轴有两条对称轴。补充：菱形的定义：有一组对边相等的平行四边形叫做菱形。

菱形的判定方法5个

菱形的判定方法5个介绍如下：方法一：根据边长判定如果一个四边形的四条边全都相等，那么这个四边形就是菱形。因为所有相邻的边都相等，所以对角线互相平分，因此对角线长度也相等。

边长与角度判定除了直接测量边长外，还可以通过计算角度来判断是否为菱形。在一个四边形中，如果相对的两角之和等于180度且所有边等长，则该四边形为菱形。这是因为相对的两角互补以及等长的边都符合菱形的几何特征。所以此判定方式是一种更为精确的识别方法。

菱形的5个判定方法如下：四条边都相等的四边形是菱形。有一组邻边相等的平行四边形是菱形。对角线互相垂直的平行四边形是菱形。对角线互相垂直且平分的四边形是菱形。有一条对角线平分一组对角的平行四边形是菱形。

在同一平面内，一组邻边相等的平行四边形是菱形；对角线互相垂直的平行四边形是菱形；四条边均相等的四边形是菱形；对角线互相垂直平分的四边形；两条对角线分别平分每组对角的四边形；有一对角线平分一个内角的平行四边形。

菱形的性质与判定是什么?

1、性质对角线互相垂直且平分，并且每条对角线平分一组对角；四条边都相等；对角相等，邻角互补；菱形既是轴对称图形，对称轴是两条对角线所在直线，也是中心对称图形，在60°的菱形中，短对角线等于边长，长对角线是短对角线的√3倍。

2、菱形性质对角线互相垂直且平分，并且每条对角线平分一组对角；四条边都相等；对角相等，邻角互补；菱形既是轴对称图形，对称轴是两条对角线所在直线，也是中心对称图形，在60°的菱形中，短对角线等于边长，长对角线是短对角线的√3倍。

3、菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的对角线互相垂直平分且平分每一组对角；菱形是轴对称图形，对称轴有2条，即两条对角线所在直线；菱形是中心对称图形。

4、判定方法：对角线性质：菱形的对角线互相垂直且平分。四边相等：菱形的四条边都相等。邻边互相垂直：菱形的邻边互相垂直。对角线等分对角：菱形的对角线将每个角平分为两个相等的角。

5、一组邻边相等的平行四边形是菱形；对角线互相垂直的平行四边形是菱形；四条边均相等的四边形是菱形；拓展：菱形性质：在一个平面内，有一组邻边相等的平行四边形是菱形。角A=C，角B=C。特殊时A、B两角也相菱形具有平行四边形的一切性质。菱形的四条边都相等。

6、菱形在几何学中是一种特殊的平行四边形，其独特之处在于它的一组邻边相等。因此，菱形不仅具备平行四边形的所有特性，还拥有额外的性质和判定条件。首先，菱形的四条边长度完全相等，这是它与其他平行四边形的主要区别之一。

菱形的判定

方法一：根据边长判定如果一个四边形的四条边全都相等，那么这个四边形就是菱形。因为所有相邻的边都相等，所以对角线互相平分，因此对角线长度也相等。此时可以用勾股定理来证明它们的长度相等，即对于菱形 ABCD，设 AC=DB=a，则有AC^2+BD^2=AD^2+BC^2=2a^2，因此AC=BD=√2a。

有一组邻边相等的平行四边形是菱形(既可以作为定理，也可以作为判定)。对角线互相垂直的平行四边形是菱形。四边相等的四边形是菱形。4 .对角线互相垂直平分的四边形是菱形。

根据菱形的定义，一组邻边相等的平行四边形是菱形。因此，可以通过测量平行四边形的四边长度，如果一组相邻边相等，则该平行四边形为菱形。性质判定菱形具有对角相等且互相垂直平分的性质。根据这一性质，可以通过测量并计算平行四边形的对角线长度及角度来判断是否为菱形。

菱形判定定理1 四边都相等的四边形是菱形菱形判定定理2 对角线互相垂直的平行四边形是菱形一定相等；不相等不是菱形。