三角形有几条对称轴（三角形有几条对称轴正确答案）

正三角形有几条对称轴

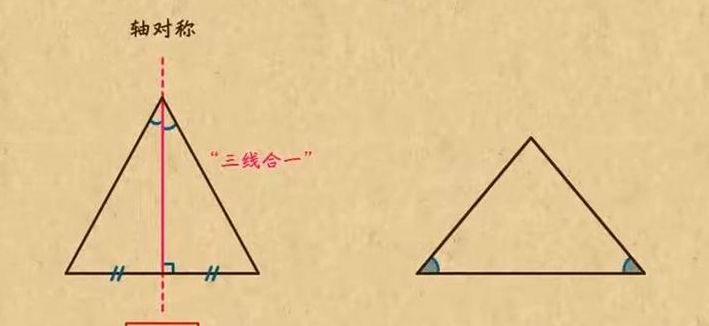
正三角形有3条对称轴。正三角形一般指等边三角形，等边三角形是轴对称图形，它有三条对称轴，对称轴是每条边上的中线、高线或角的平分线所在的直线。正三角形为三边相等的三角形，其三个内角相等，均为60°，它是锐角三角形的一种。等边三角形也是最稳定的结构。

有三条。分析：等边三角形是轴对称图形，它有三条对称轴，对称轴是每条边上的中线、高线或角的平分线所在的直线。

正三角形有3条对称轴，正三角形是轴对称图形，它有三条对称轴，对称轴是每条边上的中线、高线或角的平分线所在的直线。如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称。如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

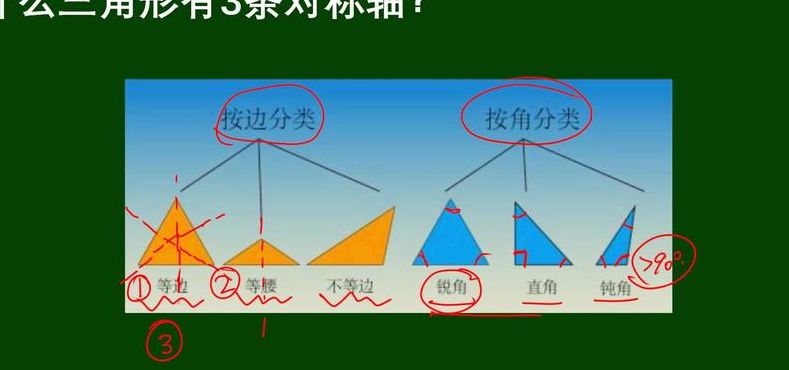
等腰三角形有一条对称轴，就是底边的中线；等边三角形有三条对称轴，就是各边的中线；等腰直角三角形有一条对称轴，就是斜边的中线；普通三角形没有对称轴。

等腰三角形有一条对称轴；等边三角形有三条对称轴。对称轴，数学名词，是指使几何图形成轴对称或旋转对称的直线。对称图形的一部分绕它旋转一定的角度后，就与另一部分重合。定理：对称轴上的任意一点与对称点的距离相等；对称点所连线段被对称轴垂直平分。

任意三角形没有对称轴；等腰三角形有一条对称轴；等边三角形有三条对称轴。

三角形对称轴的多少取决于其形状。具体而言，不等边三角形没有对称轴；等腰三角形只有一条对称轴，这条对称轴是通过顶点和底边中心的直线；等边三角形有三条对称轴，每条都经过一个顶点和与之相对的边的中点。在平面上，三角形的内角和始终等于180，这是三角形内角和定理的基本内容。

三角形有几种对称方式？以正三角形为例，它拥有三条对称轴。等边三角形是轴对称图形，其对称轴在每条边上的中线、高线或角的平分线处，通过这些轴线将三角形分为两半，两部分完全相同。在几何学中，轴对称或镜像对称意味着一个图形可以通过沿某一直线折叠，使得图形的每一点都与另一侧的对应点重合。

三角形的对称轴情况：等腰三角形有一条对称轴，就是底边的中线；等边三角形有三条对称轴，就是各边的中线；等腰直角三角形有一条对称轴，就是斜边的中线；普通三角形没有对称轴。

关于三角形有几条对称轴如下等腰三角形有一条对称轴；等边三角形有三条对称轴。对称轴，数学名词，是指使几何图形成轴对称或旋转对称的直线。对称图形的一部分绕它旋转一定的角度后，就与另一部分重合。定理：对称轴上的任意一点与对称点的距离相等；对称点所连线段被对称轴垂直平分。

1、等腰三角形有一条对称轴；等边三角形有三条对称轴。

2、等腰三角形有一条对称轴；等边三角形有三条对称轴。对称轴，数学名词，是指使几何图形成轴对称或旋转对称的直线。对称图形的一部分绕它旋转一定的角度后，就与另一部分重合。定理：对称轴上的任意一点与对称点的距离相等；对称点所连线段被对称轴垂直平分。

3、正三角形有3条对称轴，正三角形是轴对称图形，它有三条对称轴，对称轴是每条边上的中线、高线或角的平分线所在的直线。如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称。如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

4、有三条。分析：等边三角形是轴对称图形，它有三条对称轴，对称轴是每条边上的中线、高线或角的平分线所在的直线。

5、问题五：等边三角形是轴对称图形吗？它有几条对称轴解是，有三条分析：等边三角形是轴对称图形，它有三条对称轴，对称轴是每条边上的中线、高线或角的平分线所在的直线。