对数函数的性质
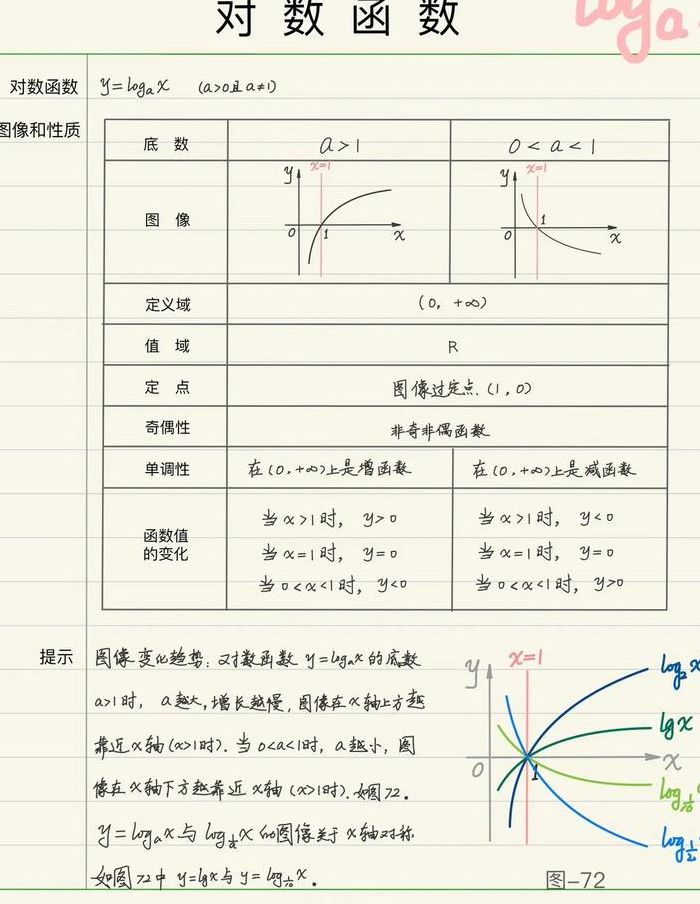
对数函数性质:值域:实数集R,显然对数函数无界;定点:对数函数的函数图像恒过定点(1,0);单调性:a1时,在定义域上为单调增函数。
一般地,对数函数以幂(真数)为自变量,指数为因变量,底数为常量的函数。对数函数是6类基本初等函数之一。其中对数的定义:如果ax=N(a0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数,其中a叫做对数的底数,N叫做真数。
对数函数的主要性质: 正数幂的性质:对数函数的真数必须为正数。这是因为对数函数的定义是基于正数的指数运算,其内部表示为一个正数的幂次。例如,log=blog。此外,对数函数的定义域是。这意味着对数函数的输入值必须大于零。 乘法性质:对数函数的乘法可以转化为加法运算。
对数函数的性质主要包括以下几点: 对数函数是指数函数的对数,即底数大于零且不等于一的真数,函数的定义域为(1,+∞)。 对数函数是单调递增的,其图像都是过点(1,0)且过该点的直线以上的无限靠近直线但永不相交的无限个点。
对数函数性质:定义域和值域 对数函数定义域为正实数集,值域为实数集。对数函数只在正数范围内有意义,这是因为对数函数的定义是基于幂运算的,其自变量必须大于零。对数函数的值域为全体实数,随着自变量的增大,函数值可以无限增大或减小。
对数函数有什么性质?
对数函数的主要性质: 正数幂的性质:对数函数的真数必须为正数。这是因为对数函数的定义是基于正数的指数运算,其内部表示为一个正数的幂次。例如,log=blog。此外,对数函数的定义域是。这意味着对数函数的输入值必须大于零。 乘法性质:对数函数的乘法可以转化为加法运算。
对数函数的主要性质有:正数幂性质:对数函数的真数要求为正数。当对数函数的自变量大于零时,其值总是实数。这是对数函数定义域和值域的特殊性质。此外,对数函数的指数与对数之间互为逆运算,这意味着底数固定的对数函数在其定义域内是单调的。底数不同时,对数函数的单调性也会有所不同。
奇偶性:对数函数是非奇非偶函数。 周期性:对数函数不是周期函数。 零点:函数的零点是x = 1。 特殊规则:经典表述“底真同对数正,底真异对数负”意味着,若y = loga b(a 0, a ≠ 1, b 0),则根据底数和真数的大小关系,对数值的正负会有所不同。
对数函数的性质主要包括以下几点: 对数函数是指数函数的对数,即底数大于零且不等于一的真数,函数的定义域为(1,+∞)。 对数函数是单调递增的,其图像都是过点(1,0)且过该点的直线以上的无限靠近直线但永不相交的无限个点。
叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。其中x是自变量,函数的定义域是(0,+∞),即x0。它实际上就是指数函数的反函数,可表示为x=ay。因此指数函数里对于a的规定,同样适用于对数函数。“log”是拉丁文logarithm(对数)的缩写。
对数函数的性质主要体现在以下几个方面:值域:对数函数的值域是实数集R,由于其无界性,其结果可以取到任何实数。图像特征:函数图像恒过一个定点,即(1,0)。这是对数函数的一个显著特性。单调性:当底数a大于1时,对数函数在定义域内单调递增;反之,0a1时,函数单调递减。
log函数的性质是什么?
1、log函数是以某个正数(底数)为底的对数函数。以下是log函数的一些主要性质: 定义域:log函数的定义域为正实数集合,即 x 0。 值域:log函数的值域为实数集合,即 (-∞, +∞)。
2、其他性质:换底公式log(a)(N)=log(b)(N)÷log(b)(a)log(a)(b)=1/log(b)(a)对数函数的图像都过(1,0)点。对于y=log(a)(n)函数 当0a1时,图像上显示函数为(0,+∞)单增,随着a的增大,图像逐渐以(0)点为轴逆时针转动,但不超过X=5。
3、log函数是指数函数的反函数。它的性质如下: 定义域:log函数的定义域是正实数集合,即x 0。 值域:log函数的值域是实数集合。 单调性:log函数是严格递增函数,即随着x的增大,log(x)也随之增大。 零点:log函数的零点是1,即log(1) = 0。
对数函数有哪些性质?怎么求导数?
1、对数函数y=logaX(a0且a≠1)的性质如下:定义域(0,+∞),值域R;图像过定点(1,0);当0a1时,在(0,+∞)上是减函数,当a1时,在(0,+∞)上是增函数。
2、对数函数的导数公式是:如果a(a0,且a≠1)的b次幂等于N,那么数b叫做以a为底N的对数,记作logaN=b,其中a叫做对数的底数,N叫做真数。对数函数的导数是1/(xlna)。
3、对数函数的求导公式如下: 对于自然对数函数 ln(x),其导数为 1/x。 对于一般形式的对数函数 log_a(x)(其中 a 0 且 a ≠ 1),其导数为 x^(-1) / ln(a)。
4、对数函数的求导公式是:d/dx(log(x))=1/x。对数函数的定义和性质 对数函数是指数函数的逆运算,表示为y=log(x)。常见的对数函数有自然对数(ln)和常用对数(log10)。对数函数具有很多重要的性质,例如log(ab)=log(a)+log(b),log(a/b)=log(a)-log(b),以及log(a^b)=b*log(a)等。
5、对数函数的导数可以表示为: 对于自然对数函数 ln(x),其导数为 1/x。 对于以 a 为底的对数函数 log_a(x)(其中 a 0 且 a ≠ 1),其导数为 1/x * ln(a)。对数函数的其他性质包括:- 当底数 a 1 时,对数函数随着真数 x 的增加而增加。
6、对数函数导数的性质 零点:对数函数的导数在x=1处为零,即dy/dx=0。求导规则 基本对数函数的导数:当函数为y=loga(x)时,其中a是一个正实数且不等于1。dy/dx=1/(xln(a))自然对数函数的导数:当函数为y=ln(x)时,其中ln表示以e为底的对数。
对数函数的运算性质
1、对数的运算性质:对数函数过定点(1,0),即x=1时,y=0。当0<a<1时,在(0,+∞)上是减函数;当a>1时,在(0,+∞)上是增函数。对数函数运算性质 一般地,如果a(a0,且a≠1)的b次幂等于N,那么数b叫做以a为底N的对数,记作logaN=b,其中a叫做对数的底数,N叫做真数。
2、对数函数有以下运算性质: 对数函数的定义域:对数函数与指数函数相反,其定义域为正实数集。 对数函数的值域:对数函数以某个底数为基数时,其值域为实数集。 对数函数的对数底变换法则:对数函数以不同的底数为基数时,可以利用换底公式进行计算和比较。
3、单调性:a1时,在定义域上为单调增函数;0a1时,在定义域上为单调减函数。奇偶性:非奇非偶函数 周期性:不是周期函数 对称性:无 最值:无 零点:x=1 注意:负数和0没有对数。两句经典话:底真同对数正,底真异对数负。