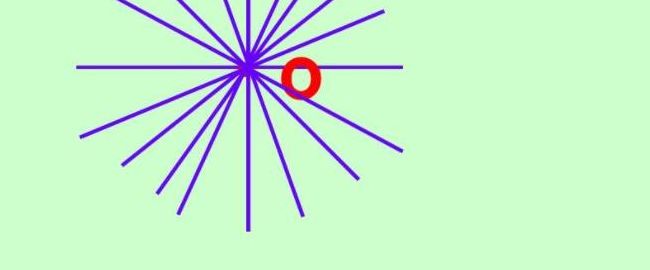
经过一点可以画几条直线
1、经过一点可以作无数条直线。 两点确定一条直线,因此过两点只能画一条直线。直线由无数个点构成,直线是面的组成成分,并继而组成体。 直线没有端点,向两端无限延长,长度无法度量。它有无数条对称轴,其中一条是它本身,还有所有与它垂直的直线(有无数条)对称轴。
2、无数条。根据两点确定一条直线的公理,过一点可以画出无数条直线。 一。过两点可以画出一条直线,且只能画一条直线。 直线的基本性质。直线的基本性质包括:- 经过两点有一条直线,并且只有一条直线。- 两条直线相交,只有一个交点。 直线概念的理解。
3、无数条。根据两点确定一条直线的公理可知:过A点可以画(无数)条直线,过A、B两点可以画(一)条直线,而且只能画一条直线。直线的基本性质(公理):(1)经过两点有一条直线,并且只有一条直线。(2)两条直线相交,只有一个交点。因为直线是不定义的名词,对直线概念的理解往往靠上述的基本性质。
4、在同一平面内经过一点可以画一条直线和已知直线垂直。若为平面上则有一条,若在空间则有无数条。
5、过一点可以画(无数)条直线,过两点可以画(一)条直线。两点确定一条直线。过两点只能画一条直线。直线由无数个点构成。直线是面的组成成分,并继而组成体。没有端点,向两端无限延长,长度无法度量。直线是轴对称图形。
过一点可以画多少条直线?可以画多少条射线?
一点可以画无数条直线,无数条射线,因为两点才能确定一条直线,一个点上有无数条直线和射线。
过一点可以画无数条线,过一点可以画无数条射线,过两点可以画一条直线,用两点为端点可以画一条线。直线的存在性和唯一性 经过两点有且只有一条直线(两点确定一条直线)在同一平面内,过直线上一点或直线外一点,能且只能引一条直线和已知直线垂直。
通过一个点可以画出无数个角。 对于射线,选择一个方向后,可以画出唯一的一条射线。 射线是起点在给定点上,沿着某个方向无限延伸的线段。 因此,通过任意一点都可以画出无数条直线和一条射线。 这个问题涉及到数学几何学中的基础概念。
从一点出发,可以画无数条射线,无数条线段,过一点可以画无数条直线,过两点可以画一条直线。判定方法:直线由无数个点构成。直线是面的组成成分,并继而组成体。没有端点,向两端无限延长,长度无法度量。直线是轴对称图形。用直尺把两点连接起来,就得到一条线段。
经过一点,可以画无数条直线,同时也画无数条射线。
经过一点可以画(无数)条射线 经过两点可以画一条直线 叫线段 直线:是一个点在平面或空间沿着一定方向和其相反方向运动的轨迹;不弯曲的线。射线是描述光线或其他电磁辐射传播的方向的一条曲线。由各种放射性核素发射出的、具有特定能量的粒子或光子束流。
过一点可以画无数条直线对吗
1、该话不对。过一点可以画无数条直线是因为直线在几何中是向两方无限延伸的,所以过一个点可以画出无数条直线。过两点也可以画无数条直线,这是因为两点确定一条直线,但是这两点之间可以有无数的直线通过它们。
2、经过一点可以作无数条直线。 两点确定一条直线,因此过两点只能画一条直线。直线由无数个点构成,直线是面的组成成分,并继而组成体。 直线没有端点,向两端无限延长,长度无法度量。它有无数条对称轴,其中一条是它本身,还有所有与它垂直的直线(有无数条)对称轴。
3、过1点可以画出无数条直线。对的!2点可以确定一条直线。
4、经过一点可以作无数条直线; 故答案为:正确。两点确定一条直线,所以过两点只能画一条直线,直线由无数个点构成。直线是面的组成成分,并继而组成体。没有端点,向两端无限延长,长度无法度量,它有无数条对称轴,其中一条是它本身,还有所有与它垂直的直线(有无数条)对称轴。
5、过一点可以画无数条直线,过两点有且只有唯一一条直线。过一个点可以画无数条直线。直线是几何学基本概念,是点在空间内沿相同或相反方向运动的轨迹。或者定义为曲率最小的曲线(以无限长为半径的圆弧)。直线有无数条对称轴,其中一条是它本身,还有所有与它垂直的直线(有无数条)对称轴。
6、过一点只能画出一条直线不对。根据直线的性质,过两点可以画一条直线,过一点可以画无数条直线。假设过一点A只能画出有限条直线,总条数设为N。(线段就不用证明,一条直线上就可以截取无数条线段。)我可以用一个球面将这个点A包裹起来,那这N条直线将穿过球面,会形成2N个点。
过一点只能画出一条直线.
1、过一点只能画出一条直线的说法是错误的,过一点能画出无数条直线。关于直线性质的相关定理介绍如下:过两点有且只有一条直线;两点之间线段最短;过一点有且只有一条直线与已知直线垂直;直线外一点与直线上各点连接的所有线段中,垂线段最短。
2、这句话是正确的。当我们说“过一点只能画一条直线”时,这种表述是不准确的。实际上,如果从一点出发,我们可以画出无数条直线。这取决于我们选择的方向和角度。所以,当我们说“过一点可以画一条直线”时,这是完全正确的。为了更好地理解这一点,我们可以想象一下一个平面。
3、在几何学中,一个点的位置确定了无数条可能的直线方向,因此通过一个点可以画出无数条直线。这反映了点与直线之间的关系非常灵活。然而,当引入第二个点时,情况发生了变化。这两个点共同定义了一条唯一的直线,这条直线是唯一能够同时通过这两个点的直线。因此,过两个点只能画一条直线。
4、过一点只能画出一条直线的说法是不准确的。实际上,过一点我们能画出无数条直线。关于直线的性质,有几个重要的定理需要了解:首先,过两点有且仅有一条直线。这意味着,如果你有两个不同的点,通过这两个点,你只能画出一条唯一的直线。其次,两点之间的线段是最短的。
5、过一点只能画出一条直线不对。根据直线的性质,过两点可以画一条直线,过一点可以画无数条直线。假设过一点A只能画出有限条直线,总条数设为N。(线段就不用证明,一条直线上就可以截取无数条线段。)我可以用一个球面将这个点A包裹起来,那这N条直线将穿过球面,会形成2N个点。
6、过一点只能画出一条直线不对。过一点能画出无数条直线。所以过一点只能画出一条直线说法错误。直线由无数个点构成,点动成线。直线是面的组成成分,并继而组成体。没有端点,向两端无限延伸,长度无法度量。直线是轴对称图形。它有无数条对称轴,对称轴为所有与它垂直的直线(有无数条)。