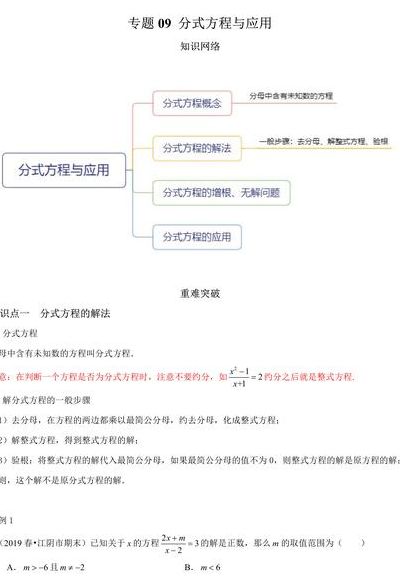
什么是“增根”?
增根:数学名词,是指在分式方程化为整式方程的过程中,若整式方程的根使最简公分母为0,(根使整式方程成立,而在分式方程中分母为0)那么这个根叫做原分式方程的增根。举例:x/(x-2)-2/(x-2)=0 解:去分母,x-2=0 x=2 但是X=2使分母等于0(无意义),所以X=2是增根。
增根就是使分式原方程的分母为零的X的值,例如:1/3X-3,当X等于1时,分母为零,则X=1是原分式方程的增根。
增根就是指,在对方程进行变化过程中没有施行同解变形而导致方程增加的根。有时也会有漏根。如 √x=x-2 ,两边平方得 x=x^2-4x+4 ,所以 x^2-5x+4=0 ,(x-1)(x-4)=0 ,根为 1 和 4 ,此时 x=1 的根即是增根 。在解 x=x^2 时,两边同除以 x 得 x=1 。
增根是什么
1、增根:增根,是指方程求解后得到的不满足题设条件的根。一元二次方程与分式方程和其它产生多解的方程在一定题设条件下都可能有增根。在分式方程化为整式方程的过程中,分式方程解的条件是使原方程分母不为零。
2、增根是一个数学用语,其定义为在方程变形时,有时可能产生不适合原方程的根。
3、增根是指让分式方程无意义的根。比如分式方程2/(x-1)-1/(x-1)=0,按分式方程的解法,解出来x=1,但x=1却使原方程没有意义,那么x=1就是增根。
增根是什么意思?
定义:在 方程变形时 ,有时 可能 产生 不适合 原方程的 根 ,这种根叫做原方程的 增根 。
增根,是指方程求解后得到的不满足题设条件的根。一元二次方程与分式方程和其它产生多解的方程在一定题设条件下都可能有增根。在分式方程化为整式方程的过程中,分式方程解的条件是使原方程分母不为零。
增根是一个中文词语,意思是指在原来的基础上增加根数或根源,使之更加牢固、稳定或深入。在不同的领域中,都可以使用这个词来表示增强、加强或加深某种程度或因素。
所谓“增根”,就是这个根代入原方程,使得原方程中的分母等于0或带开平方根的式子没有意义的根。
增根是指方程求解后得到的不满足题设条件的根。增根的产生原因:对于分式方程,当分式中,分母的值为零时,无意义,所以分式方程,不允许未知数取那些使分母的值为零的值,即分式方程本身就隐含着分母不为零的条件。
增根(increasing roots)是指一个方程有多个根,且这些根是逐渐增加的。例如,方程^23+2=0的根是=1和=2,根是增根的。无解(no solution)是指一个方程没有任何解。例如,方程^2+1=0没有实数解,因为平方数加一不可能等于零。这种情况下,方程被称为无解。
什么是增根
1、增根:增根,是指方程求解后得到的不满足题设条件的根。一元二次方程与分式方程和其它产生多解的方程在一定题设条件下都可能有增根。在分式方程化为整式方程的过程中,分式方程解的条件是使原方程分母不为零。
2、增根是指让分式方程无意义的根。比如分式方程2/(x-1)-1/(x-1)=0,按分式方程的解法,解出来x=1,但x=1却使原方程没有意义,那么x=1就是增根。
3、定义:在 方程变形时 ,有时 可能 产生 不适合 原方程的 根 ,这种根叫做原方程的 增根 。
数学中“增根”是什么意思
增根,指方程求解后得到的不满足题设条件的根。一元二次方程与分式方程和其它产生多解的方程在一定题设条件下都可能有增根。在分式方程化为整式方程的过程中,分式方程解的条件是使原方程分母不为零。
增根在数学中指的是让分式方程失去意义的根。比如分式方程2/(x-1)-1/(x-1)=0,按照分式方程的解法,解出x=1。但x=1使原方程没有意义,那么x=1就是增根。增根是针对分式方程、根式方程等方程的。对于分式方程,去分母后得到的方程解中,若存在使得原方程无意义的解,则这个解是增根。
增根是指让分式方程无意义的根。在方程变形时,有时可能产生不适合原方程的根,这种根叫做原方程的增根。如果一个分式方程的根能使此方程的公分母为零,那么这个根就是原方程的增根。
数学增根是一个常用的数学词汇,它的意思是在已知的根的基础上,再添加一个新的根来求解问题。通常,在解决高次方程和其他复杂问题时,数学增根的方法是非常有效的。通过增加一个根,我们可以获得更多的信息和更准确的答案。当然,数学增根并不是万能的方法,有时候它仍然无法解决某些特殊的问题。