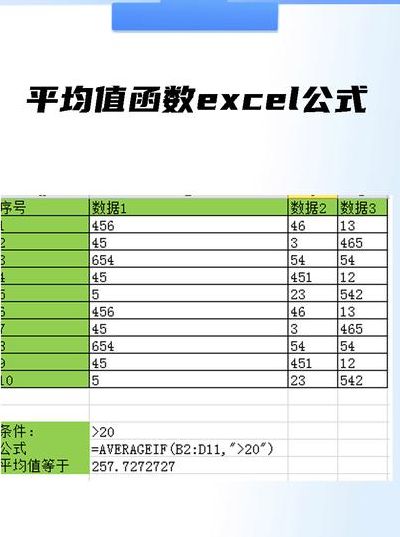
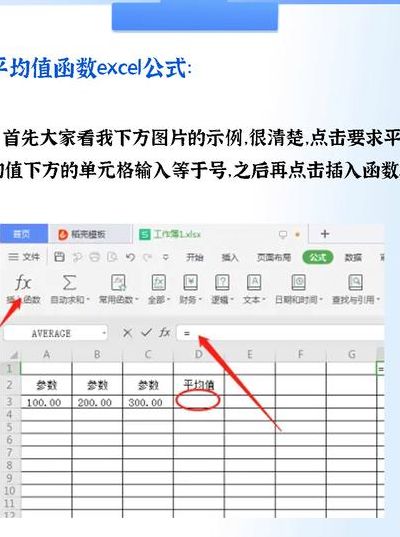
算术平均值怎么求
算术平均数的基本公式:M=(X1+X2+...+Xn)/n。算术平均数,又称均值,主要适用于数值型数据。算术平均值主要适用于数值型数据,不适用于品质数据。根据表现形式的不同,算术平均值有不同的计算形式和计算公式。简单算术平均:主要用于未分组的原始数据。
算术平均值是指将一组数据相加后除以数据的个数所得的值。具体计算方法为:(1)将一组数据按从小到大的顺序排列。(2)计算数据个数n。(3)将数据相加,即sum=a1+a2+a3+…+an。(4)将数据之和除以数据个数,即平均值=sum/n。
简单的算术平均数的计算公式为:加权平均数的公式如下,w为各个事件的概率 用法不同:在实际问题中,当各项权重不相等时,计算平均数时就要采用加权平均数;当各项权相等时,计算平均数就要采用算术平均数。
算术平均值怎么算
1、简单算术平均:主要用于末分组的原始数据。设一组数据为X1,X2,...n,简单的算术平均值的计算公式为:M(X1+X2+...+Xn)/n。加视算术平均:主要田于外理经分组警理的数程,没原始教挥为被分水组。
2、算术平均数的基本公式:M=(X1+X2+...+Xn)/n。算术平均数,又称均值,主要适用于数值型数据。算术平均值主要适用于数值型数据,不适用于品质数据。根据表现形式的不同,算术平均值有不同的计算形式和计算公式。简单算术平均:主要用于未分组的原始数据。
3、简单的算术平均数的计算公式为:加权平均数的公式如下,w为各个事件的概率 用法不同:在实际问题中,当各项权重不相等时,计算平均数时就要采用加权平均数;当各项权相等时,计算平均数就要采用算术平均数。
4、算术平均值是指将一组数据相加后除以数据的个数所得的值。具体计算方法为:(1)将一组数据按从小到大的顺序排列。(2)计算数据个数n。(3)将数据相加,即sum=a1+a2+a3+…+an。(4)将数据之和除以数据个数,即平均值=sum/n。
5、算数平均值的一般公式是:算术平均数是统计学中最基本、最常用的一种平均指标,分为简单算术平均数、加权算术平均数。算术平均值主要适用于数值型数据,不适用于品质数据,根据表现形式的不同,算术平均数有不同的计算形式和计算公式。
算术平均值的公式是什么?
1、算术平均值的公式是平均值 = 总和 / 数量。算术平均值,也叫均值,是一组数值中所有数值的累加和除以数值的个数得出的结果。此公式为计算平均值的基本方法。
2、算术平均数的基本公式为:M=(X1+X2+...+Xn)/n。这里的M代表算术平均数,XX...、Xn表示一组数值数据,n则是这组数据的个数。算术平均数常被用来描述一组数值数据的一般水平,它是统计中一个重要的统计量,用来描述数据集的中心趋势。
3、算数平均值公式:M=(X1+X2+…+Xn)/n 算术平均数,又称均值,是统计学中最基本、最常用的一种平均指标,分为简单算术平均数、加权算术平均数。它主要适用于数值型数据,不适用于品质数据。根据表现形式的不同,算术平均数有不同的计算形式和计算公式。
4、主要用于末分组的原始数据。设一组数据为X1,X2,...n,简单的算术平均值的计算公式为:M(X1+X2+...+Xn)/n。加视算术平均:主要田于外理经分组警理的数程,没原始教挥为被分水组。
什么叫算术平均,几何平均值,加权平均值
1、算术平均值,又称为简单平均值,是一组数值的总和除以数值的个数。它是日常生活中最为常见和直观的平均值计算方法。例如,如果有三个数:4和6,那么它们的算术平均值就是(2+4+6)/3=4。
2、算术平均、几何平均和加权平均值是数学和统计学中常用的三种平均值计算方法。具体解释如下:算术平均 算术平均是将一组数值的总和除以数值的数量。这是计算平均值的简单方法,适用于数据之间相互差异不大且不具有特殊结构性的数据。公式表示为:平均值 = 总和 / 数量。
3、在数学统计中,有三种常见的平均值概念:算术平均值、几何平均值和加权平均值。它们用来度量一组数值的整体趋势,但计算方法各有不同。首先,算术平均值,也称为简单平均,是最直观的一种。例如,如果我们有两个数A和B,它们的算术平均值就是(A+B)除以2。
4、算术平均数:算术平均数是指在一组数据中所有数据之和再除以数据的个数。它是反映数据集中趋势的一项指标。几何平均数:n个观察值连乘积的n次方根就是几何平均数。根据资料的条件不同,几何平均数分为加权和不加权之分。调和平均数:调和平均数是平均数的一种。
5、平均数主要有三种类型:算术平均数、几何平均数和加权平均数。 算术平均数 算术平均数是所有数值的和除以数值的个数得到的。这是最常见的一种平均数计算方法。例如,在一组数据中,将所有的数据相加后除以数据的总数,即可得到算术平均数。其计算公式为:算术平均数 = 。
6、fk叫做权。 说明:1)“权”的英文是weight,表示数据的重要程度。即数据的权能反映数据的相对“重要程度”。 2) 平均数是加权平均数的一种特殊情况,即各项的权相等时,加权平均数就是算术平均数。
几何平均值和算术平均值的区别有哪些?
1、几何平均值和算术平均值:从计算方法、数据处理方式、应用领域、数据特征、加权平均值来进行区别。计算方法:算术平均值:算术平均值是一组数据中所有数值之和除以数据个数得到的平均值。计算公式为:平均值 = 总和 / 数据个数。
2、二者公式的形式不同:二者的含义不同:算术平均数( arithmetic mean),又称均值,是统计学中最基本、最常用的一种平均指标,分为简单算术平均数、加权算术平均数。它主要适用于数值型数据。几何平均数是对各变量值的连乘积开项数次方根。求几何平均数的方法叫做几何平均法。
3、算术平均值和几何平均值的区别在于计算方法和应用领域不同。算术平均值是一组数值之和除以数值的个数,用于表示一组数据的集中趋势。它适用于各种情况,包括统计数据、考试成绩等。算术平均值的计算公式为总和除以个数。几何平均值是一组数值的乘积的n次方根,其中n为数值的个数。
4、几何平均值是n个变量值连乘积的n次方根,而算术平均值是数值型数据总和除以数据的个数。以下是两者的详细对比:几何平均值: 定义:几何平均数是n个变量值连乘积的n次方根。
伯努力方程实验
这就是伯努利方程,此式虽然是从不可压缩的液体如水的情况中推出来的,但对一切流体均适用。由此式可得当y1=y2时,谁的速度越大压强越少。(很抱歉,昨晚我打字时分心了,把方程的原理“动能定理”打成了“机械能守恒”。
伯努利方程:p+ρgz+(1/2)*ρv^2=C 式中p、ρ、v分别为流体的压强、密度和速度;h为铅垂高度;g为重力加速度;c为常量。一个直接的结论就是:流速高处压力低,流速低处压力高。
伯努利效应,源于D.伯努利在1738年的贡献,是描述理想正压流体在势能场中定常运动时机械能守恒的基本原理。当流体沿流线运动,欧拉方程积分后,我们得到了著名的伯努利方程。
比如,管道内有一稳定流动的流体,在管道不同截面处的竖直开口细管内的液柱的高度不同,表明在稳定流动中,流速大的地方压强小,流速小的地方压强大。这一现象称为“伯努利效应”。伯努力方程:p+1/2pv^2=常量。在列车站台上都划有安全线。
伯努力原理如下:丹尼尔·伯努利在1726年提出了“伯努利原理”。这是在流体力学的连续介质理论方程建立之前,水力学所采用的基本原理,其实质是流体的机械能守恒。即:动能+重力势能+压力势能=常数。其最为著名的推论为:等高流动时,流速大,压力就小。
伯努利微分方程是p+1/2ρv2+ρgh=C。伯努力的定律是在一个流体系统,比如气流、水流中,流速越快,流体产生的压强就越小,这就是被称为“流体力学之父”的丹尼尔·伯努利1738年发现的“伯努利定理”。