矩阵迹的定义是什么
1、矩阵的迹就是主对角元元素之和,两矩阵的迹相同显然就是两个矩阵各自的主对角元元素之和是相等的。且矩阵的迹有以下常用性质:迹是所有对角元的和,迹是所有特征值的和。某些时候也利用tr(AB)=tr(BA)来求迹。
2、矩阵的迹是一个数学概念,指的是一个方阵的主对角线元素的总和。详细解释如下:矩阵的基本概念 矩阵是一个由数值组成的矩形阵列,通常用于线性代数、数值分析和计算机科学等领域。矩阵中的元素按照一定的行和列进行排列。方阵是矩阵的一种特殊情况,其行数和列数相等。
3、设有N阶矩阵A,那么矩阵A的迹(用表示)就等于A的特征值的总和,也即矩阵A的主对角线元素的总和。迹是所有对角元的和。迹是所有特征值的和。某些时候也利用tr(AB)=tr(BA)来求迹。tr(mA+nB)=mtr(A)+ntr(B)。
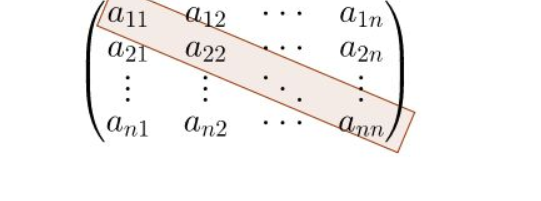
4、矩阵的迹是对角线元素的总和。对于一个n阶方阵,其主对角线上的元素依次为a11,a22,…,ann,矩阵的迹Tr就定义为这些元素的总和,即Tr = a11 + a22 + … + ann。由于操作简便且意义明确,这一特性在线性代数的研究中尤为重要。矩阵的迹与特征值的关系 矩阵的迹与其特征值之间存在密切关系。
5、迹,是线性代数中的概念,矩阵的迹:主对角线(左上至右下的那一条)上所有元素之和。记作tr(A),其中A为方阵。若A为C*代数,ρ为A的态,则A的一个归一化的迹为一个非平凡可迹态。矩阵的迹:主对角线(左上至右下的那一条)上所有元素之和。记作tr(A),其中A为方阵。
6、矩阵的迹是指矩阵主对角线上元素的和,通常用tr(A)表示。矩阵的迹有以下性质: 对于任意矩阵A和B,有tr(A+B) = tr(A) + tr(B)。这个性质可以通过展开矩阵的主对角线上的元素并进行简单的运算得到。 对于任意矩阵A和B,有tr(AB) = tr(BA)。
什么是矩阵的迹?
1、设有N阶矩阵A,那么矩阵A的迹(用表示)就等于A的特征值的总和,也即矩阵A的主对角线元素的总和。迹是所有对角元的和。迹是所有特征值的和。某些时候也利用tr(AB)=tr(BA)来求迹。tr(mA+nB)=mtr(A)+ntr(B)。
2、矩阵的迹是一种特殊的数值,用于描述矩阵的重要属性。具体来说,矩阵的迹是指矩阵所有特征值之和。这一概念在矩阵理论、线性代数、数值计算等领域中具有重要的应用价值。关于矩阵的迹的详细解释如下:矩阵特征值与迹的概念关联 在矩阵理论中,特征值和迹是两个紧密相关的概念。
3、tr表示矩阵的迹,在线性代数中,一个n×n矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数),一般记作tr(A)。
请教矩阵的迹是什么?
1、矩阵的迹指:在线性代数中,一个n×n矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数),一般记作tr(A)。
2、迹是所有对角元的和。迹是所有特征值的和。某些时候也利用tr(AB)=tr(BA)来求迹。tr(mA+nB)=mtr(A)+ntr(B)。
3、在线性代数中,tr(A)代表一个方阵A的迹,也称为矩阵的迹。矩阵的迹是指矩阵主对角线上各个元素的和。具体来说,对于一个n × n的方阵A,其迹可以表示为:tr(A) = A[1, 1] + A[2, 2] + ... + A[n, n]其中A[i, j]表示矩阵A的第i行第j列的元素。
4、迹是所有对角元的和;迹是所有特征值的和;某些时候也利用tr(AB)=tr(BA)来求迹;tr(mA+nB)=m tr(A)+n tr(B)。
矩阵的迹是什么
1、迹,是线性代数中的概念,矩阵的迹:主对角线(左上至右下的那一条)上所有元素之和。记作tr(A),其中A为方阵。若A为C*代数,ρ为A的态,则A的一个归一化的迹为一个非平凡可迹态。矩阵的迹:主对角线(左上至右下的那一条)上所有元素之和。记作tr(A),其中A为方阵。
2、矩阵的迹指:在线性代数中,一个n×n矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数),一般记作tr(A)。
3、设有N阶矩阵A,那么矩阵A的迹(用表示)就等于A的特征值的总和,也即矩阵A的主对角线元素的总和。迹是所有对角元的和。迹是所有特征值的和。某些时候也利用tr(AB)=tr(BA)来求迹。tr(mA+nB)=mtr(A)+ntr(B)。
4、矩阵的迹是一个数学概念,指的是一个方阵的主对角线元素的总和。详细解释如下:矩阵的基本概念 矩阵是一个由数值组成的矩形阵列,通常用于线性代数、数值分析和计算机科学等领域。矩阵中的元素按照一定的行和列进行排列。方阵是矩阵的一种特殊情况,其行数和列数相等。
5、方阵A的迹tr(A)=a11+a22+...+ann,即等于对角线元素和。迹是所有对角元的和;迹是所有特征值的和;某些时候也利用tr(AB)=tr(BA)来求迹;tr(mA+nB)=m tr(A)+n tr(B)。
6、多个矩阵相乘得到的方阵的迹,和将这些矩阵中的最后一个挪到最前面之后相乘的迹是相同的。将一个矩阵分解为比较简单或者性质比较熟悉的矩阵之组合,方便讨论和计算。由于矩阵的特征值和特征向量在化矩阵为对角形的问题中占有特殊位置, 因此矩阵的特征值分解。
矩阵的迹是什么?有什么性质?
矩阵的迹是一个矩阵的对角线元素之和。详细解释如下:矩阵的迹的定义 矩阵的迹是指矩阵中所有对角线元素的和。对于一个nn的矩阵A,其迹记作tr,数学上表示为:tr = aii,其中i从1到n,aii表示矩阵A第i行第i列的元素。换句话说,矩阵的迹就是其主对角线上元素的总和。
迹是所有对角元的和;迹是所有特征值的和;某些时候也利用tr(AB)=tr(BA)来求迹;tr(mA+nB)=m tr(A)+n tr(B)。
矩阵的迹指:在线性代数中,一个n×n矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数),一般记作tr(A)。
矩阵的迹是指线代数中矩阵的主对角线上各个元素的总和;矩阵的迹拥有的质为:矩阵的迹是所有对角元的和,矩阵的迹也是所有特征值的和,若矩阵有N阶,则矩阵的迹就等于矩阵的特征值的总和,也即矩阵的主对角线元素的总和。
矩阵的迹是指矩阵主对角线上元素的和,通常用tr(A)表示。矩阵的迹有以下性质: 对于任意矩阵A和B,有tr(A+B) = tr(A) + tr(B)。这个性质可以通过展开矩阵的主对角线上的元素并进行简单的运算得到。 对于任意矩阵A和B,有tr(AB) = tr(BA)。