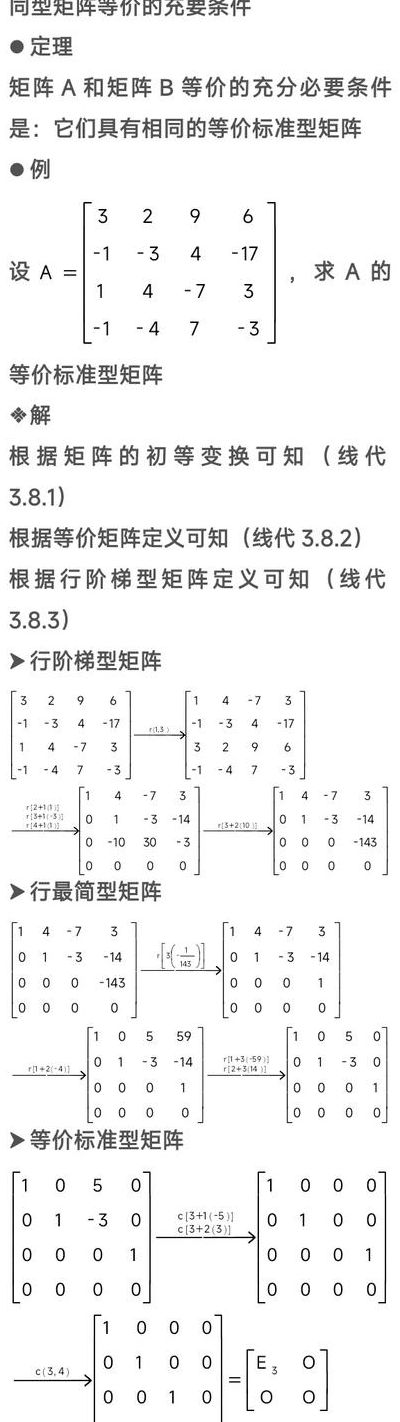
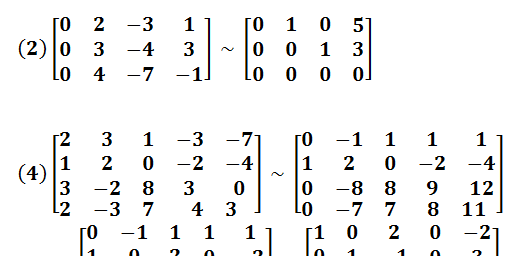标准型矩阵是什么?
1、标准形矩阵:矩阵的标准形是左上角为单位矩阵, 其余子块为0 的分块矩阵。矩阵标准型的理论来自于矩阵的相似性,矩阵在初等变化下有很多数值不一样的表象,但其本质特征,特征多项式等都是相同的,这些相似不变量就是这个矩阵的本质特征。
2、矩阵标准型是:如果矩阵B可以由A经过一系列初等变换得到 那么矩阵A与B是等价的。若矩阵A能与对角形矩阵相似,那么该对角形矩阵的对角线元素是A的n个特征值而且可逆矩阵p的列向量就是对应于这些特征值的n个线性无关的特征向量。
3、矩阵的标准形:由m×n个数aij排成的m行n列的数表称为m行n列的矩阵,具体如下:这m×n 个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n,m×n矩阵A也记作Amn。
4、标准形矩阵:每个非零行的第一个非零元素为1,每个非零行的第一个非零元素所在列的其他元素全为零,则是最简形矩阵。如果一个矩阵的左上角为单位矩阵,其他位置的元素都为零。在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合,最早来自于方程组的系数及常数所构成的方阵。
实对称矩阵的标准形与规范形有哪些区别?
系数不同标准型:标准型的系数可以为任意常数。规范型:规范型的系数只能为-1,0,1。转化不同标准型:同一实对称矩阵A化为的标准型可以有多个。规范型:同一实对称矩阵A化为的规范型是唯一的。
首先,从系数的角度来看,标准型的系数可以为任意常数,这意味着在化为标准型的过程中,平方项的系数可以是任何实数。而规范型则更为严格,其系数只能为-0或1。这种限制使得规范型在形式上更为统一和简洁。其次,在转化方式上,同一实对称矩阵A可以化为多个不同的标准型,这取决于所采用的线性变换。
系数不同 标准型:标准型的系数可以为任意常数。规范型:规范型的系数只能为-1,0,1。转化不同 标准型:同一实对称矩阵A化为的标准型可以有多个。规范型:同一实对称矩阵A化为的规范型是唯一的。
标准型和规范型的区别主要体现在系数、转化以及所有项的不同上。首先,从系数的角度来看,标准型的系数可以为任意常数,这意味着在标准型中,各项的权重可以是多种多样的,没有特定的限制。而规范型则不同,它的系数只能为-0或1,这种限制使得规范型在表达上更为统一和规范。
系数不同。标准型:标准型的系数可以为任意常数。规范型:规范型的系数只能为-1,0,1。转化不同。标准型:同一实对称矩阵A化为的标准型可以有多个。规范型:同一实对称矩阵A化为的规范型是唯一的。平方项的系数不同。
标准型矩阵一定是方阵吗
1、标准型矩阵一定是方阵。如果矩阵B可以由A经过一系列初等变换得到,那么矩阵A与B是等价的。经过多次变换以后,得到一种最简单的矩阵,就是这个矩阵的左上角是一个单位矩阵,其余元素都是0,那么这个矩阵就是原来矩阵的等价标准型。矩阵的运算 是数值分析领域的重要问题。
2、矩阵不同:在构成矩阵时,标准型系数矩阵一定是一个方阵,在构成矩阵时,不是所有情况下都能得到一个方阵作为系数。
3、不是,标准型不唯一,规范型唯一,两者矩阵均不唯一。矩阵(Matrix)指在数学中,按照长方阵列排列的复数或实数集合,最早来自于方程组的系数及常数所构成的方阵,由19世纪英国数学家凯利首先提出。它是高等代数学中的常见工具,其运算是数值分析领域的重要问题。
4、标准形矩阵:每个非零行的第一个非零元素为1,每个非零行的第一个非零元素所在列的其他元素全为零,则是最简形矩阵。如果一个矩阵的左上角为单位矩阵,其他位置的元素都为零。
什么叫矩阵的标准型啊?
1、矩阵标准型是:如果矩阵B可以由A经过一系列初等变换得到 那么矩阵A与B是等价的。若矩阵A能与对角形矩阵相似,那么该对角形矩阵的对角线元素是A的n个特征值而且可逆矩阵p的列向量就是对应于这些特征值的n个线性无关的特征向量。
2、矩阵的标准形是左上角为单位矩阵, 其余子块为0 的分块矩阵。如果矩阵B可以由A经过一系列初等变换得到 那么矩阵A与B是等价的 经过多次变换以后,得到一种最简单的矩阵,就是这个矩阵的左上角是一个单位矩阵,其余元素都是0,那么这个矩阵就是原来矩阵的等价标准型。
3、矩阵的等价标准型是指将一个矩阵通过一系列的行变换和列变换转化为一个特定的形式,这个形式具有一定的性质,可以用来描述矩阵的某些特征。具体来说,矩阵的等价标准型有以下几种: 行简化阶梯形矩阵:矩阵的每一行都有且仅有一个非零元素,且这个非零元素在每一行中的位置都比上一行靠右。