一阶导数和二阶导数的区别和联系有什么?
二阶导数是一阶导数的导数,从原理上,它表示一阶导数的变化率;从图形上看,它反映的是函数图像的凹凸性。导数:导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。
当一阶导数和二阶导数都等于0时,该点为驻点。二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f(x)的导数yˊ=fˊ(x)仍然是x的函数,则y′′=f′′(x)的导数叫做函数y=f(x)的二阶导数。在图形上,它主要表现函数的凹凸性。
一阶导数为零且二阶导数大于零表示极小值点;一阶导数为零且二阶导数小于零则表示极大值点。 实际问题的应用:在物理学中,二阶导数描述加速度的变化;经济学中分析成本和收益的变化率随时间的变化;在优化问题中,二阶导数辅助确定函数曲率,指导选择合适的优化策略。
一阶导数用于描述函数的增减性。简单来说,如果一阶导数为正,函数在此区间内是递增的;如果为负,则是递减的。二阶导数则用来判断函数的凹凸性。具体来说,当二阶导数大于零时,函数在该区间内是凹的;当二阶导数小于零时,函数在该区间内是凸的。这一性质在优化问题和曲线拟合中有重要应用。
一阶导数反映的是函数斜率,而二阶导数反映的是斜率变化的快慢,表现在函数的图像上就是函数的凹凸性。f′′(x)0,开口向上,函数为凹函数,f′′(x)0,开口向下,函数为凸函数。
一阶导数和二阶导数都是描述函数变化率的概念,但它们的计算和含义有所不同。一阶导数(也称为导数或一阶导数)描述了函数在每个点上的切线斜率。它表示了函数的变化速率或增减性。一阶导数可以通过计算函数的斜率来获得,对应于函数的斜率函数。
二阶导数为什么能保证一阶导数存在?
二阶导数是在一阶导数的基础上再求一次导数,所以肯定能保证一阶导数的存在性。
具体来说,如果函数在某点二阶可导,意味着存在两个连续的极限:一阶导数的极限和二阶导数的极限。根据二阶导数极限的存在性,可以推导出一阶导数在该点连续。一阶导数在该点连续意味着,函数在该点的邻域内至少存在一个一阶导数,即函数在该邻域内一阶可导。
首先探讨一种理解,即函数在某点的二阶导数存在时,意味着该函数在此点的邻域内存在一阶导数。从逻辑上推断,既然函数的二阶导数在某点存在,则其一阶导数在该点必然连续,连续性确保了该一阶导数在邻域内也得以存在,进一步说明,原函数在该点的邻域内确实具有连续的一阶导数。
总结,二阶可导性确实可以说明一阶导函数在该点领域内可导。这一结论基于导数存在的连续性与函数导数在连续区间内的性质。通过深入理解这些数学概念,我们可以更准确地分析函数的行为,以及在特定点的性质。
一阶导数的连续性是二阶导数存在的必要条件,因此一阶导数连续时,二阶导数必定存在。 然而,一阶导数的存在并不保证二阶导数的存在。例如,如果一阶导数在某点不连续,那么该点二阶导数就不存在。 同样,如果一阶导数存在但某个更高阶的导数不连续,那么这个更高阶的导数就不存在。
一阶导数和二阶导数分别是什么?
1、简单来说,一阶导数是自变量的变化率,二阶导数就是一阶导数的变化率,也就是一阶导数变化率的变化率。连续函数的一阶导数就是相应的切线斜率。一阶导数大于0,则递增;一阶倒数小于0,则递减;一阶导数等于0,则不增不减。而二阶导数可以反映图象的凹凸。
2、一阶和二阶在数学和物理领域中,分别代表一阶导数和二阶导数。一阶导数:定义:函数在某一点的导数即为该点处的一阶导数,它描述了函数值随自变量变化的速率。意义:一阶导数零,如同汽车动力的瞬间转折点,意味着可能存在的极值点,代表着动力释放的微妙平衡。
3、一阶导数和二阶导数都是描述函数变化率的概念,但它们的计算和含义有所不同。一阶导数(也称为导数或一阶导数)描述了函数在每个点上的切线斜率。它表示了函数的变化速率或增减性。一阶导数可以通过计算函数的斜率来获得,对应于函数的斜率函数。
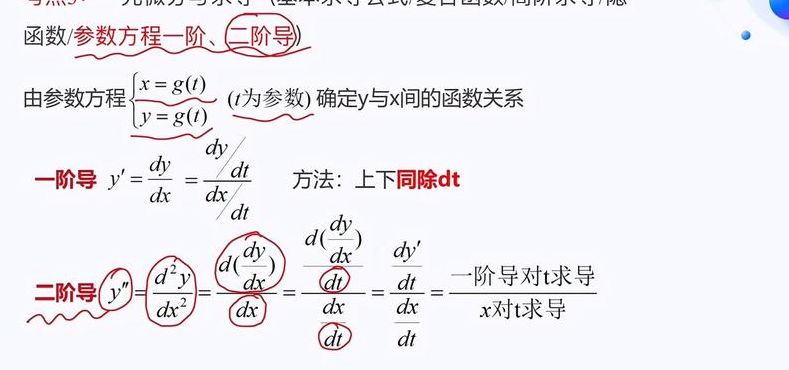
4、dx和dx的区别如下图所示:二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f(x)的导数yˊ=fˊ(x)仍然是x的函数,则y′′=f′′(x)的导数叫做函数y=f(x)的二阶导数。在图形上,它主要表现函数的凹凸性。
5、一阶导数反映的是函数斜率,而二阶导数反映的是斜率变化的快慢,表现在函数的图像上就是函数的凹凸性。f′′(x)0,开口向上,函数为凹函数,f′′(x)0,开口向下,函数为凸函数。
二阶导数与一阶导数之间的相互转化关系是什么?
两者相关转化如下:将x看作自变量,y看作因变量时,y对x的二阶导数可以转化为x对y的一阶导数,即d^2y/dx^2=d/dy(dy/dx)=d/dy(x)。同理,将y看作自变量,x看作因变量时,x对y的二阶导数可以转化为y对x的一阶导数,即d^2x/dy^2=d/dx(dx/dy)=d/dx(y)。
当一阶导数和二阶导数都等于0时,该点为驻点。二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f(x)的导数yˊ=fˊ(x)仍然是x的函数,则y′′=f′′(x)的导数叫做函数y=f(x)的二阶导数。在图形上,它主要表现函数的凹凸性。
二阶导函数即一阶导数的导数,可以判断出一阶导数的增减性,驻点二阶导数值0→以驻点(一阶导数=0的点)为中心的邻域内,一阶导数单调递增,驻点的导数值=0→驻点两侧,一阶导数的值左-右+→驻点为原函数的极小值点。
原函数f(x)经过一次求导得到它的导函数f(x),这个导函数仍然是函数,当然可以继续对它求导,这样就得到它的二阶导数f(x)。可导的条件:如果一个函数的定义域为全体实数,即函数在实数域上都有定义,答案是否定的。函数在定义域中一点可导需要一定的条件。
二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f(x)的导数yˊ=fˊ(x)仍然是x的函数,则y′′=f′′(x)的导数叫做函数y=f(x)的二阶导数。在图形上,它主要表现函数的凹凸性。几何意义 切线斜率变化的速度,表示的是一阶导数的变化率。
一阶导数与二阶导数的关系
1、当一阶导数和二阶导数都等于0时,该点为驻点。二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f(x)的导数yˊ=fˊ(x)仍然是x的函数,则y′′=f′′(x)的导数叫做函数y=f(x)的二阶导数。在图形上,它主要表现函数的凹凸性。
2、两者相关转化如下:将x看作自变量,y看作因变量时,y对x的二阶导数可以转化为x对y的一阶导数,即d^2y/dx^2=d/dy(dy/dx)=d/dy(x)。同理,将y看作自变量,x看作因变量时,x对y的二阶导数可以转化为y对x的一阶导数,即d^2x/dy^2=d/dx(dx/dy)=d/dx(y)。
3、原函数f(x)经过一次求导得到它的导函数f(x),这个导函数仍然是函数,当然可以继续对它求导,这样就得到它的二阶导数f(x)。可导的条件:如果一个函数的定义域为全体实数,即函数在实数域上都有定义,答案是否定的。函数在定义域中一点可导需要一定的条件。
4、二阶导函数即一阶导数的导数,可以判断出一阶导数的增减性,驻点二阶导数值0→以驻点(一阶导数=0的点)为中心的邻域内,一阶导数单调递增,驻点的导数值=0→驻点两侧,一阶导数的值左-右+→驻点为原函数的极小值点。
5、二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f(x)的导数yˊ=fˊ(x)仍然是x的函数,则y′′=f′′(x)的导数叫做函数y=f(x)的二阶导数。在图形上,它主要表现函数的凹凸性。几何意义 切线斜率变化的速度,表示的是一阶导数的变化率。
6、探讨二阶导数与一阶导数的关系,当二阶导数大于零,一阶导数呈现单调递增特性。二阶导数是基于一阶导数的再导,若其值为正,说明一阶导数随变量变化持续递增。取一阶导数的边界值,最小为零时,可以推断出二阶导数始终大于零。这意味着,通过二次求导并比较边界值,可以判断原函数单调递增。