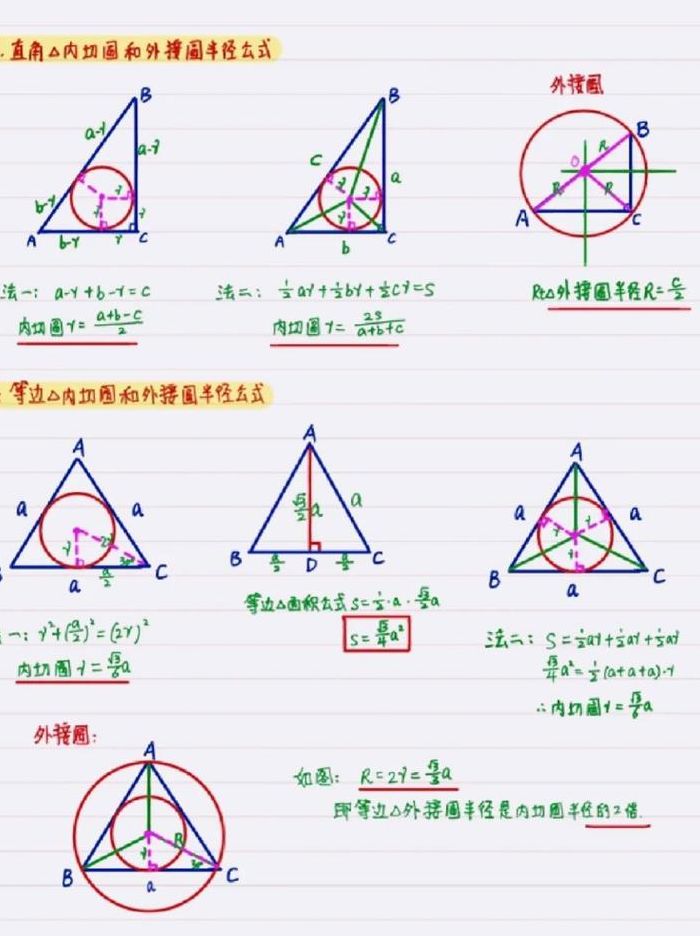
圆的半径怎么求出来的?
1、通过圆的面积来计算出其半径。以下是具体的步骤:首先,我们需要知道圆的面积公式是πr,其中r是圆的半径,π是一个常数,约等于14159。然后,如果你已经知道了圆的面积A,你可以通过这个公式来求解半径r。将面积A代入公式,得到r=√(A/π)。这就是求解半径的公式。
2、圆的半径可以通过圆的周长来计算哦:圆的半径 = 圆的周长 ÷ 2 ÷ π。具体步骤:先量出圆的周长:想象一下,你手里有个圆圈圈,你得拿根线绕它一圈,然后量出这根线的长度,这就是圆的周长啦。然后除以2:把量出来的周长除以2,这样你就得到了圆的直径。
3、圆的半径可以通过以下方式求解:使用周长计算半径:圆的周长公式为:C = 2πr,其中C代表圆的周长,r代表半径。已知周长C,可以变形公式求解半径r,即:r = C / 。圆周率π的取值:圆周率π是一个特定的数值,约等于14。
4、圆的一般方程半径为:r=√(D+E-4F)/2,利用圆的周长公式求半径,r=C/2π,利用圆的面积公式求半径,r=√(S/π)。
5、做AB的垂直平分线,交圆弧于C,连接AC,过A做AC的垂线,交AB的垂直平分线于D。CD就是圆的直径,找到CD的中点O,OC就是半径。
圆的圆心坐标公式和半径公式分别是什么
1、圆的圆心坐标公式:r=√[(D^2+E^2-4F)]/2,圆的半径公式:r=√[(x-a)^2+(y-b)^2]。圆是一种特殊的曲线,它既是轴对称图形,又是中心对称图形,圆的任意一条直径所在的直线都是它的对称轴,圆心是它的对称中心,而且一个圆绕圆心旋转任意一个角度,都能与原来的图形重合。
2、圆在标准方程式下的圆心坐标为:(a,b),半径公式为:r=√[(x-a)^2+(y-b)^2]。圆在一般方程式下的圆心坐标为:(-D/2,-E/2),半径公式为:r=√[(D^2+E^2-4F)]/2。
3、圆的一般方程为 x+y+Dx+Ey+F=0 (D+E-4F0),或可以表示为(X+D/2)+(Y+E/2)=(D+E-4F)/4。其中圆心坐标是:(-D/2,-E/2)。半径:1/2√(D+E-4F)。
4、圆心坐标的公式是利用圆的三个系数D, E, F来确定的,即r = √[(D * E - 4F)] / 2。这个公式展示了圆心位置与给定圆的系数之间的关系。
5、圆一般式的圆心和半径公式介绍如下:圆的一般方程:x+y+Dx+Ey+F=0(D+E-4F0),圆心:(-D/2,-E/2),半径:根号(D+E-4F)/2。
圆的半径怎么算?
公式:圆的半径 = 周长 ÷ ,其中π约等于14。说明:如果你知道一个圆的周长,可以用这个公式来计算它的半径。通过直径计算:公式:圆的半径 = 直径 ÷ 2。说明:直径是穿过圆心、两端都在圆上的线段。如果你知道一个圆的直径,可以直接将其除以2来得到半径。
半径 = 周长 ÷ 2 ÷ π(14)圆的方程:圆的标准方程:在平面直角坐标系中,以点O(a,b)为圆心,以r为半径的圆的标准方程是(x-a)^2+(y-b)^2=r^2。圆的一般方程:把圆的标准方程展开,移项,合并同类项后,可得圆的一般方程是x^2+y^2+Dx+Ey+F=0。
计算圆半径:方法 1: 已知直径计算圆半径;计算公式是:D = 2r。其中“D”代表直径,“r”代表半径。公式可变换为r = D/2。方法 2: 已知周长求半径;周长公式是C= 2πr,其中“r”代表半径,π是圆周率(14.)。换算成半径公式就是r = C/2π。
圆的半径=周长÷2π(14),圆或圆的半径是从其中心到其周边的任何线段,并且在更现代的使用中,它也是其中任何一个的长度。这个名字来自拉丁半径,意思是射线,也是一个战车的轮辐。半径的复数可以是半径(拉丁文复数)或常规英文复数半径。半径的典型缩写和数学变量名称为r。