根号30开出来是多少
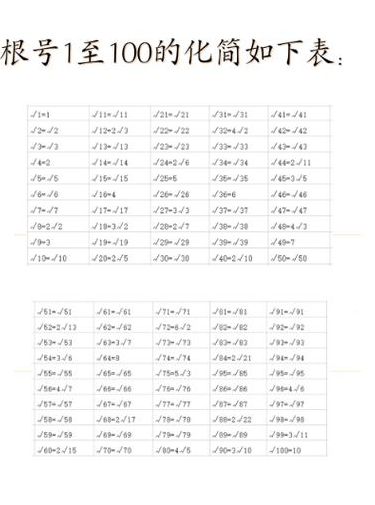
√30=√(3×10)=√(3×2×5),其中,5 都不是完全平方数根号30不能化简了,30可分解为2乘3乘5 ,而2,3,5中没有一个完全平方数所以不能化简。所以,根号30已是最简根式。开平方根先开最里面的根号然后再开最外面的根号。开根号的方法:因式分解法。
根号30的正确计算方法 根号30属于一个无理数,因此不能够再进行继续化简,但可以通过计算器的形式进行计算,首先在计算器上面按出30,然后再按一个根号,可以得出结果根号30≈48。或者可以利用逼近的方法求出根号30的一个大概取值范围,根号30大于根号25小于根号36,因此根号30的取值范围在5到6之间。
根号30等于477。根据查询相关信息显示,根号30等于47722557505,约等于477。30的因数有30,都不能够完整的开出一个平方,比如根号8等于2倍根号2,是因为八的因数有2×4,根号4等于是可以开根号等于2,因此根号30不能化简,可以≈48。
根号30等于多少?
根号30等于477。根据查询相关信息显示,根号30等于47722557505,约等于477。30的因数有30,都不能够完整的开出一个平方,比如根号8等于2倍根号2,是因为八的因数有2×4,根号4等于是可以开根号等于2,因此根号30不能化简,可以≈48。
。根据查询数学查表法的法则得知,根号30等于47722557505,小数点保留后三位是48。30的因数有30,都不能够完整的开出一个平方,如根号8等于2倍根号2,8的因数有2乘以4,根号4等于是可以开根号等于2,因此根号30不能化简,可以开出根号是48。
约等于477。由于根号30是一个无理数,我们无法得到精确的结果。因此,我们只能使用近似值来表示。根号30表示30的平方根,这个数学表达式的含义是,求一个数,使得这个数的平方等于30,即30的0.5次方约等于477。
根号30约等于±478。与30相邻的完全平方数是5的平方25和6的平方36,36-30>30-25,因此根号值小于5与6的中间值5。两个数的差距非常接近,可以从45开始验证。
根号30等于47722557505,约等于477,30的因数有30,都不能够完整的开出一个平方,比如根号8等于2倍根号2,是因为八的因数有2乘4,根号4等于是可以开根号等于2,根号30不能化简,可以约等48。
根号三十等于多少
1、约等于477。30的因数有30,都不能够完整的开出一个平方,比如8=2*4,√4=2,所以√8=2√2,而√30不能化简,所以√30≈48。根号是一个数学符号。根号是用来表示对一个数或一个代数式进行开方运算的符号。
2、根号化简,就是通俗情况下的开平方,30的因数有1,2,3,5,6,10,15,30。这些因数都不能是某一个数的平方,所以根号三十不能再继续化简。根号化简一般是找某一个数的最大因数,要是这个最大因数能够是某一个数的平方,那便再好不过了,就可以直接化简。
3、。根据幂指数函数的性质我们知道253036,所以这个无理数介于56之间,因为无理数的计算量都是非常大的,我们通过计算器得到本题大约等于4772。根号三十约等于4772,其实就是把一个无理数约等于一个有理数的问题,考虑到取值问题,我们都会取小数点后面四位。
4、等于(ab)/10 因为根号3=a,根号30=b 所以可以根据以上条件理解为 根号0.9=根号3*0.3 ,根号30=根号3*10=√[(3×10)/(10)]就是想办法把未知的根号0.9转换成已知的根号3和根号30,这样就全是已知的了,能解答了。
由根号3的值约为1.732,不用计算器怎样求根号30的值
√3≈732 √3是一个无理数,它的小数部分是无限不循环的,无论算多久也算不出小数部分的规律。但是√3不一定只能用计算器算出结果,它的大致结果也能通过手算算出。
手动开平方 手动开立方 设A = X^3,求X.称为开立方。
根号3≈732只能用计算器运算,如果自己算只能得出近似值。开根也叫开方,指求一个数的方根的运算,为乘方的逆运算(参见“方根”词条),在中国古代也指求二次及高次方程(包括二项方程)的正根。在实数范围内,负数无法开偶次根。正根又称算数根。
为了得到更精确的值,我们可以使用长除法。使用长除法计算:在长除法中,将三作为被除数,初始商为二,然后进行计算,逐步调整商的值,直到得到满意的结果。通过这种方式,我们可以得到根号三的近似值。现在,借助计算器,我们可以更容易、更快速地得到根号三的值约为732。
根号3≈732。根号3是一个无理数,它的小数部分是无限不循环的,无论算多久也算不出小数部分的规律。但是根号3不一定只能用计算器算出结果,它的大致结果也能通过手算算出。
号6=根号2X根号3,已知根号3约等于4149 所以根号600的近似值为24,根号2约等于449x10=24,根号6约等于2。