三角形的外接圆怎么画,图解
1、选择“线段直尺工具”,做出三角形ABC,具体如图所示。依次选择线段AB、线段BC,画出这两条边的中点D、E,具体如图所示。做线段AB、线段BC的垂直平分线,相交于O点,连接OE和DE,具体如图所示。以OB作为圆的半径,画出三角形的外接圆,具体如图所示。
2、步骤1,画△ABC边AB的垂直平分线DE,如下图:步骤画△ABC边BC的垂直平分线FG,交DE与H,如下图:步骤H就是外接圆的圆心,以H为圆心,以HA为半径画圆H,圆H就是三角形ABC的外接圆,如下图:圆H就是三角形ABC的外接圆。
3、以三角形ABC为例:作线段AB的垂直平分线L。作线段BC的垂直平分线与直线L交于O。以点O为圆心,以OA的长为半径作圆即可。做其中两条边条边的垂直平分线,以此交点为圆心。分别以线段两端为圆心,以大于线段1/2为半径在线段两侧作弧,连两相交点,此线就是该线段的垂直平分线。
4、用圆规作等边三角形的外接圆:如图,在等边三角形任意两边各作一条垂直平分线,两条垂直平分线的交点就是外接圆圆心,这时以该交点和三角形任意一角的连线为半径作圆,即为该三角形的外接圆。
5、首先,使用“线段直尺工具”绘制三角形ABC,如图所示。接着,选取线段AB和BC,分别标出它们的中点D和E,如图所示。然后,作出线段AB和BC的垂直平分线,这两条线相交于点O。接着,连接点O和E,以及点O和D,如图所示。以点O为圆心,OB为半径画出三角形的外接圆,如图所示。
绝缘子控件的定义是什么
绝缘子或称为边缘元件,是特殊的顺式作用元件。其作用只是阻止激活或遏制作用在染色质上的传递,因而使染色质活性限定于结构域之内。如果将一个绝缘子置于增强子和启动子之间,它能阻止增强子对启动子的激活。另一方面,如果一个绝缘子在活性基因和异染色质之间,它可以保护基因免受异染色质化扩展招致的失活。
绝缘子,这一生物学概念,是一种在基因调控序列中占据关键位置的分子。它的长度大约在几百个核苷酸对范围内,最短时甚至仅有42个碱基对。作为顺式作用元件,绝缘子的主要特性在于其中性调控,它位于基因表达的调控过程中,起到了分隔器的作用。
绝缘子是一种特殊的绝缘控件,在架空输电线路中扮演重要角色。早年间,绝缘子主要用于电线杆,现今发展为高压电线连接塔的一端挂有许多盘状绝缘体,用于增加爬电距离,通常由玻璃或陶瓷制成。绝缘子能够承受环境和电负荷变化带来的机电应力,避免因失效而导致整条线路的使用和运行寿命受损。
三角形外接圆的性质有哪些
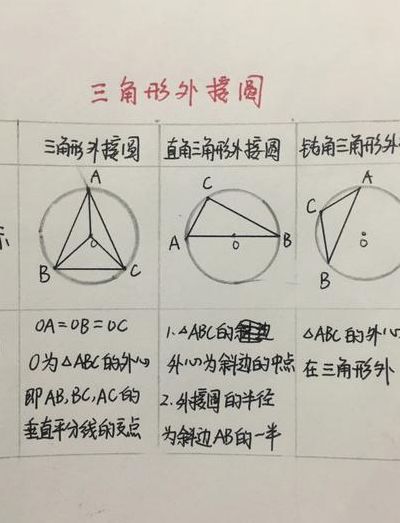
1、三角形的外接圆的性质:外接圆的圆心到三角形的三个顶点的距离相等。锐角三角形外心在三角形内部。直角三角形外心在三角形斜边中点上。钝角三角形外心在三角形外。
2、三角形外接圆的性质有哪些如下:性质1:锐角三角形的外心在三角形内;直角三角形的外心在斜边上,与斜边中点重合;钝角三角形的外心在三角形外.等边三角形外心与内心为同一点。性质2:∠BGC=2∠A。性质3:∠GAC+∠B=90°。
3、三角形外接圆的性质有:三角形外接圆的圆心是三角形外心,外心到三角形三个顶点的距离相等。三角形外接圆的半径是三角形外心到任意一个顶点的距离。三角形内心、垂心、重心和外心四个点共圆,即在三角形外接圆上。
4、三角形的外接圆具有以下几个重要性质。1外心性质:三角形的外接圆圆心称为外心,是三角形各边垂直平分线的交点。外心到三角形各顶点的距离相等。位置关系:锐角三角形的外心位于三角形内部。直角三角形的外心位于斜边的中点上。钝角三角形的外心位于三角形外部。
5、三角形的外接圆具有一个重要性质:它的圆心到三角形的三个顶点的距离相等。 三角形的外接圆是通过连接三角形三边的垂直平分线并找到它们的交点来确定的,这个交点即是圆心。 外接圆的圆心,也称为外心,位于三角形内部,并且到三角形的三个顶点的距离相等。
三角形的外接圆
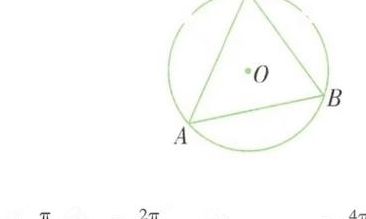
设圆的一般方程为x^2+y^2+Dx+Ey+F=0。由该圆过已知三角形的三个顶点,将三个顶点坐标代入圆的一般方程。得到关于D,E,F的三元一次方程组,解得D,E,F即可。三角形任意两边的垂直平分线,两个垂直平分线的交点就是三角形外接圆的圆心。
步骤1,画△ABC边AB的垂直平分线DE,如下图:步骤画△ABC边BC的垂直平分线FG,交DE与H,如下图:步骤H就是外接圆的圆心,以H为圆心,以HA为半径画圆H,圆H就是三角形ABC的外接圆,如下图:圆H就是三角形ABC的外接圆。
选择“线段直尺工具”,做出三角形ABC,具体如图所示。依次选择线段AB、线段BC,画出这两条边的中点D、E,具体如图所示。做线段AB、线段BC的垂直平分线,相交于O点,连接OE和DE,具体如图所示。以OB作为圆的半径,画出三角形的外接圆,具体如图所示。
三角形的外接圆具有一个重要性质:它的圆心到三角形的三个顶点的距离相等。 三角形的外接圆是通过连接三角形三边的垂直平分线并找到它们的交点来确定的,这个交点即是圆心。 外接圆的圆心,也称为外心,位于三角形内部,并且到三角形的三个顶点的距离相等。
三角形的外接圆圆心即三角形的外心,可通过公式直接求得。该公式在数学文献中普遍可见。公式如下:若将圆的方程式代入三个三角形顶点坐标,则可形成矩阵方程式。该矩阵方程式等价于行列式方程。通过行列式展开,可得到与圆方程式等效的表达式。对比该表达式与圆心方程式,可解得外心坐标。