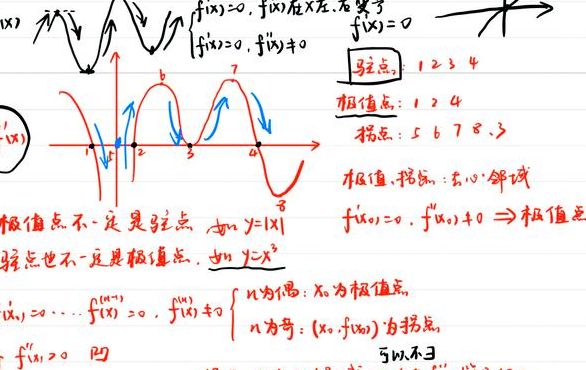
拐点是点还是坐标
1、拐点指的是函数图像上某点的横纵坐标,表示该点处函数曲线的凹凸性发生变化。驻点则是指函数的一阶导数为零的点,通常对应的是函数图像的水平切线,其横坐标值标志着函数在该点的斜率为零。
2、拐点是函数图像上的一个特殊点,通常用坐标来表示。在数学中,拐点是指函数图像上的一个点,它两侧的曲线斜率发生变化的点。也可以说,拐点是函数曲线由凸转凹或由凹转凸的点。在几何意义上,拐点是函数图像上的一个转折点。
3、拐点是坐标。拐点是一个点,由横坐标和纵坐标组成,如点(a,b)。在连续曲线上,凹凸部分的分界点称为曲线的拐点。若某点同时满足以下两个条件,则可以判定为拐点:函数在该点处的二阶导数为0;在该点的左右两边的二阶导数异号。
4、拐点是坐标。拐点是曲线上的一点,它有横坐标和纵坐标,不要只把横坐标当成拐点。拐点,又称反曲点,在数学上指改变曲线向上或向下方向的点,直观地说拐点是使切线穿越曲线的点(即连续曲线的凹弧与凸弧的分界点)。
5、在地质勘探和矿区划分中,拐点坐标扮演着重要角色。比如在地质图上,一个正方形区块的四个角点,其地理坐标即为该区块的拐点坐标,例如:33度15分30秒/106度20分45秒,这就是一个具体点。多个这样的点连接起来形成一个闭合图形,这些点则被称为拐点。
6、拐点是曲线上的一点,它有横坐标和纵坐标,不要只把横坐标当成拐点。拐点,又称反曲点,在数学上指改变曲线向上或向下方向的点,直观地说拐点是使切线穿越曲线的点(即连续曲线的凹弧与凸弧的分界点)。可以按下列步骤来判断区间I上的连续曲线y=f(x)的拐点:⑴求f(x)。
拐点,驻点,极值点分别是点还是极坐标
拐点指的是函数图像上某点的横纵坐标,表示该点处函数曲线的凹凸性发生变化。驻点则是指函数的一阶导数为零的点,通常对应的是函数图像的水平切线,其横坐标值标志着函数在该点的斜率为零。
二是利用函数的性质,包括一阶导数和二阶导数等的性质,判断函数的单调性、奇偶性、周期性和凸性等,结合关键点,如极值点、最值点、拐点、零点、与y轴的交点等,画出函数的图像。最后一种方法是利用计算器软件画出函数图像。这当然是最省力的方法了。
在函数取得极值处,曲线上的切线是水平的,但曲线上有水平曲线的地方,函数不一定取得极值,即可导函数的极值点必定是它的驻点(导数为0的点),但函数的驻点却不一定是极值点。
平方 平方是一种运算,比如,a的平方表示a×a,简写成a,也可写成a×a(a的一次方乘a的一次方等于a的2次方),例如4×4=16,8×8=64,平方符号为2。立方 立方也叫三次方。三个相同的数相乘,叫做这个数的立方。如5×5×5叫做5的立方,记做5。
什么是拐点?
1、定义:拐点,又称反曲点,在数学上指改变曲线向上或向下方向的点,直观地说拐点是使切线穿越曲线的点(即曲线的凹凸分界点)。意义:若该曲线图形的函数在拐点有二阶导数,则二阶导数在拐点处异号(由正变负或由负变正)或不存在。二阶导数,是原函数导数的导数,将原函数进行二次求导。
2、拐点的定义是二阶导数为零和不存在。这里表达的是二阶导数为零和不存在。首先拐点在数学上指改变曲线向上或向下方向的点,直观地说拐点是使切线穿越曲线的点(即曲线的凹凸分界点),若该曲线图形的函数在拐点有二阶导数,则二阶导数必为零或不存在。
3、零点,驻点,极值点指的都是函数y=f(x)的一个横坐标x0,而拐点指的是函数y=f(x)图像上的一个点。拐点:二阶导数为零,且三阶导不为零;驻点:一阶导数为零或不存在。极值点:若f(a)是函数f(x)的极大值或极小值,则a为函数f(x)的极值点,极大值点与极小值点统称为极值点。
地理中拐点的定义是什么?
在地质勘探和矿区划分中,拐点坐标扮演着重要角色。比如在地质图上,一个正方形区块的四个角点,其地理坐标即为该区块的拐点坐标,例如:33度15分30秒/106度20分45秒,这就是一个具体点。多个这样的点连接起来形成一个闭合图形,这些点则被称为拐点。
地理中拐点的定义是指地理现象或数据在变化过程中,出现的与常规趋势或预期方向相反的转折点。拐点在地理学中具有重要意义,以下是 拐点在地理现象中普遍存在。在自然现象如气候变化、地形地貌的演变中,拐点的出现常常代表着某种过程的转折点或临界点。
地理中的拐点定义为指变化发生的地方或情况发生根本性转折的地点。在地理坐标系统中,拐点则是指地理坐标数据变化的转折点。具体来说,拐点是地理数据序列中,从一个变化趋势转变为另一个变化趋势的特定点。例如,在描述气温变化趋势时,由降温转为升温的交叉点即为拐点。
当我们在处理如地质图上区块划分时,区块四个边缘的特定地理位置就被定义为拐点坐标。例如,33度**分**秒/10表怕进酸言发财况6度**分**秒,这样的坐标点就是一个拐点。如果多个这样的点通过连接形成一个封闭的图形,那么这些点就共同构成了拐点。
定义:拐点坐标通常指的是一个区块的四个角落的地理坐标。这些坐标点按照特定顺序连接可以形成一个封闭的图形。作用:定位与划分:拐点坐标在矿产资源管理和地质勘探中起到了定位和划分矿区范围的作用。开采计划:技术人员通过拐点坐标能够准确地追踪和管理资源分布,从而有效地进行开采作业。
每个区块通常由四个或更多这样的拐点通过连接形成一个封闭的图形。这些交汇点,也就是拐点,对于区块的划分和识别至关重要。在地质勘查和开采规划中,拐点坐标系统是确保精确划分和定位区块的关键工具。
拐点,驻点,极值点分别是点还是指坐标?
1、拐点指的是函数图像上某点的横纵坐标,表示该点处函数曲线的凹凸性发生变化。驻点则是指函数的一阶导数为零的点,通常对应的是函数图像的水平切线,其横坐标值标志着函数在该点的斜率为零。
2、前者是指点的坐标。即拐点是二维空间的点,其几何意义是坐标平面的点。用有序数对表示。后两者是一维空间的点,其几何意义是数轴上的点。用一个实数表示。
3、拐点、驻点、极值点都是指具体的点,而不是坐标。拐点是函数图像上凸凹性发生改变的点。在微积分中,拐点是函数图像上凸凹性发生改变的点,它标志着函数在该点处的弯曲方向发生了变化。
4、拐点,驻点均是指点,而极值点则是X轴上的横坐标。拐点,又称反曲点,在数学上指改变曲线向上或向下方向的点,直观地说拐点是使切线穿越曲线的点(即连续曲线的凹弧与凸弧的分界点)。若该曲线图形的函数在拐点有二阶导数,则二阶导数在拐点处异号(由正变负或由负变正)或不存在。
5、零点,驻点,极值点指的都是函数y=f(x)的一个横坐标x0,而拐点指的是函数y=f(x)图像上的一个点。拐点:二阶导数为零,且三阶导不为零;驻点:一阶导数为零或不存在。极值点:若f(a)是函数f(x)的极大值或极小值,则a为函数f(x)的极值点,极大值点与极小值点统称为极值点。
6、驻点和零点是x,极值点和拐点是坐标(x,y)。我们把导数f(x)的零点(即方程f(x)=0的根)叫做函数的驻点,也称临界点、稳定点,驻点可能是函数的极值点,在“这一点”,函数的输出值停止增加或减少,对于一维函数的图像,驻点的切线平行于x轴,对于二维函数的图像,驻点的切平面平行于xy平面。