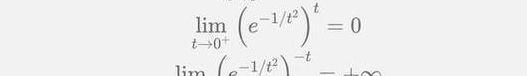零的零次方到底是1还是0
1、在数学上,任何非零实数的零次方都等于1,这是因为零次方表示对这个数进行零次乘法操作,而任何数乘以1都等于它自身。因此,对于任何非零实数x来说,x^0=1。而当基数x为0时,0^0是一个特殊情况,在数学上没有一个确定的定义。
2、零的零次方等于1。详细解释如下:在数学中,零的零次方是一个特殊的情况。我们知道,任何非零实数的零次方都是1。这是因为,根据乘方的定义,a的0次方等于a乘以自己0次,即a^0 = a a^,可以简化为a^0 = a除以自身,这就相当于任何数乘以或除以同一个数本身都等于该数的倒数或自己。
3、在数学中并没有这个说法。原因是0次方,说明除数为0;0不能作为除数。并且任何自然数的零次方为1。0的0次方的值是悬而未决的,在某些领域定义为1,某些领域未定义。不定义的理由多是以连续性为考量,不定义不连续点。
为什么0的0次方无意义
的0次方(0^0)之所以在数学中常常被视为无意义或者不确定的形式,是因为它涉及到两个基本的数学原则之间的冲突,这两个原则在0^0的情况下不能同时被满足。让我们来看一下这两种情况:指数为0的规则:根据指数法则,任何非零数字的0次幂等于1。即对于所有 a≠0a=0,有 a0=1a0=1。
的0次方在数学中通常被认为无意义,主要原因如下:基本数学规律:在数学中,除0以外的其他数的零次方都被定义为1。如果0的零次方也等于1,那么它将与数的基本规律产生冲突,因为无论多少个0相乘,其结果都应为0,而不是1。
的零次方没有意义是因为无论几个零相乘结果都应是零,而数学中把除0以外的其他数的零次方定为1,若0的零次方也等于1就不符合数的基本规律,即0没有零次方。0的0次方是悬而未决的,在某些领域定义为某些领域不定义(无意义)。定义的理由是它在某些领域有用处,方便化简公式。
在数学中,0的0次方并不无意义,但它是一个不明确或未定义的表达式。这个表达式在数学的不同领域中有不同的解释和规定。在实数和复数系统中,0的0次方被定义为1。这是基于数学中一个重要的性质,即零的乘积法则。根据这个法则,任何数与0相乘都等于0。
的0次方没有意义是因为它在数学上是一个不确定的形式。首先,让我们理解什么是0的0次方。它表示的是0个数相乘的结果。例如,10的3次方是1000,因为10乘以10乘以10等于1000。类似地,0的3次方是0,因为0乘以0乘以0还是0。但是,0的0次方表示的是0个数相乘,这在数学上是一个不确定的概念。
0的0次方是0还是1还是无意义?
的0次方无意义。因为0不能做分母。0是介于-1和1之间的整数。是最小的自然数,也是有理数。0既不是正数也不是负数,而是正数和负数的分界点。0没有倒数,0的相反数是0,0的绝对值是0。0的平方根是0,0的立方根是0,0乘任何数都等于0,除0之外任何数的0次方等于1。
的0次方在数学中通常被认为无意义,主要原因如下:基本数学规律:在数学中,除0以外的其他数的零次方都被定义为1。如果0的零次方也等于1,那么它将与数的基本规律产生冲突,因为无论多少个0相乘,其结果都应为0,而不是1。
结论是:0的0次方在数学中被认为是无意义的。让我们深入理解为什么。首先,0作为最小的自然数,具有独特的性质。它既不是正数也不是负数,被视为正负数的分界点。由于0没有倒数,其相反数和绝对值都等于自身。
0的0次方结果是0还是1还是无意义还是其他值
的0次方在数学中通常被认为无意义,主要原因如下:基本数学规律:在数学中,除0以外的其他数的零次方都被定义为1。如果0的零次方也等于1,那么它将与数的基本规律产生冲突,因为无论多少个0相乘,其结果都应为0,而不是1。
的0次方(0^0)之所以在数学中常常被视为无意义或者不确定的形式,是因为它涉及到两个基本的数学原则之间的冲突,这两个原则在0^0的情况下不能同时被满足。让我们来看一下这两种情况:指数为0的规则:根据指数法则,任何非零数字的0次幂等于1。即对于所有 a≠0a=0,有 a0=1a0=1。
的零次方没有意义是因为无论几个零相乘结果都应是零,而数学中把除0以外的其他数的零次方定为1,若0的零次方也等于1就不符合数的基本规律,即0没有零次方。0的0次方是悬而未决的,在某些领域定义为某些领域不定义(无意义)。定义的理由是它在某些领域有用处,方便化简公式。
结论是:0的0次方在数学中被认为是无意义的。让我们深入理解为什么。首先,0作为最小的自然数,具有独特的性质。它既不是正数也不是负数,被视为正负数的分界点。由于0没有倒数,其相反数和绝对值都等于自身。
0的任意次方是等于0还是1
1、的任意次方等于多少,这取决于具体的次数。当0的次幂是0时,结果无定义。而当次数为正整数时,0的任意正整数次方都等于0。若次数为负整数,则结果无意义,因为在数学中不允许除以0。所以,除了0的0次方外,0的正整数次方都是0。例如,0^1 = 0, 0^2 = 0, 以此类推。
2、的任意次方,除了0的0次方在数学上存在争议以外,其它情况下都等于0。详细来说,如果我们有一个数a,且a不等于0,那么a的任意次方都不会等于0。这是因为我们在不断地将a乘以自己,而a本身不是0,所以结果也不会是0。但是,0是一个特殊的数,因为0乘以任何数都等于0。
3、的正数次方等于0 。0的0次方等于1。 0的负数次方无意义。
4、的任意次方(除0次方外)是都等于0的,0的0次方没有意义。
5、的任何次方都等于1。这是数学中的一个基本原则,被称为“零的幂”。当我们将0乘以自身0次方时,即0^0,结果是不确定的。在数学中,0^0 是一个有争议的问题,在不同的数学领域和应用中存在不同的观点。一些学者和领域倾向于把 0^0 定义为1,而另一些则认为它没有明确定义。
6、的任意次方(0次方除外)均有意义,都等于0。0的0次方没有意义。
0的0次方是多少,为什么是1?
1、的任何次方都等于1。这是数学中的一个基本原则,被称为“零的幂”。当我们将0乘以自身0次方时,即0^0,结果是不确定的。在数学中,0^0 是一个有争议的问题,在不同的数学领域和应用中存在不同的观点。一些学者和领域倾向于把 0^0 定义为1,而另一些则认为它没有明确定义。
2、的0次方是悬而未决的,在某些领域定义为某些领域不定义(无意义)。在传统的数学观点中,0^0被定义为1。这个定义源于乘法的单位元概念,即任何数与1相乘,结果仍为其本身。0作为乘法单位元,满足这一定义。然而,在某些数学系统和应用中,0^0会被定义为0。
3、次幂只针对非零数,任何非零数的0次方都等于1,0的0次方无意义。