锥形侧面积公式计算公式
锥形侧面积公式计算公式是Πr*l。关于锥形的计算公式 圆锥的侧面积=母线的平方×π×(360分之扇形的度数)==1/2×母线长×底面周长=π×底面圆的半径×母线。
S=πRL(R为圆锥体底面圆的半径,L为圆锥的母线长)。圆锥的侧面积=(圆周率×母线长×圆心角度数)÷180 。
全面积=丌r(r+l)(L是圆锥的母线长,r是圆锥半径)方法:侧面积可以看成三角形,即运用微分的方法分成n个细细长长的小三角,当n无限大时, 三角形的面积之和就是扇形面积。
圆锥的侧面积公式是什么?
圆锥侧面积的计算公式:圆锥的侧面积=(圆周率×母线长×圆心角度数)÷180。立体几何定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。旋转轴叫做圆锥的轴。
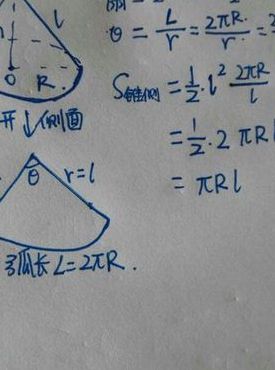
将圆锥的侧面沿母线展开,是一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长. 圆锥的侧面积就是弧长为圆锥底面的周长×母线/2;没展开时是一个曲面。
圆锥的侧面积计算公式:S侧=(1/2)*α*l=π*r*l(r:表示底面半径,l:圆锥母线,α:侧面展开图圆心角弧度)。
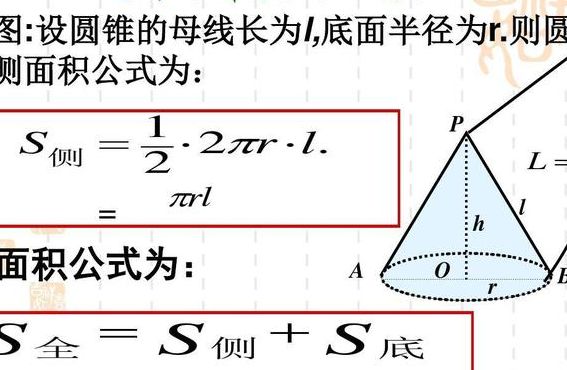
圆锥的侧面积公式等于:圆周率与圆锥底面半径、圆锥母线长的乘积。如果圆周率是Pi,圆锥底面半径是r,圆锥母线长是l,那么圆锥的侧面积等于Pi、r、l的乘积,即Pi*r*l。
圆锥的侧面积公式是S=πrL。r是圆锥底面的半径,L是圆锥的母线长,圆锥的侧面积是扇形,扇形的弧长是圆锥的底面周长2πr,展开后扇形的半径为母线L,所以扇形的面积为S=Lr/2=πrL。圆的面积是πr。
圆锥的侧面积公式是什么呢?
圆锥体的侧面积公式出现两种:S=1/2RL(R为圆锥体底面圆的周长,L为圆锥的母线长)S=πRL(R为圆锥体底面圆的半径,L为圆锥的母线长)都是正确的,只是途径不一样。
S=πrl 圆锥侧面积公式是S=πrl。其中r为底面半径,l为圆锥母线。圆锥是以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体。
公式一:S=nπR/360公式二:S=1/2LR 解释:圆锥侧面积展开是一个扇形。①n代表扇形圆心角的度数。R代表这个扇形所在圆的半径。②L是扇形的弧长,R为半径。
圆锥侧面积计算公式
1、圆锥的侧面积计算公式:S侧=(1/2)*α*l=π*r*l(r:表示底面半径,l:圆锥母线,α:侧面展开图圆心角弧度)。
2、圆锥的侧面积计算公式是S=πRL。圆锥是一个立体图形,它是由一个直角三角形把它的任意直角边作为转轴,斜边作为圆锥的母线,三百六十度旋转得出的图形,它的底边是由另一直角边旋转得到的圆形。
3、S圆锥侧=(1/2)(2r)l=rl 圆锥侧面积公式为S圆锥侧=(1/2)(2πr)l=πrl。设圆锥的底面半径为r,高为h,母线长为l(l^=r^+h^);圆锥侧面展开图是一个扇形,半径为l,弧长为2πr。
圆锥的侧面积公式是多少
S=πrl 圆锥侧面积公式是S=πrl。其中r为底面半径,l为圆锥母线。圆锥是以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体。
公式一:S=nπR/360公式二:S=1/2LR 解释:圆锥侧面积展开是一个扇形。①n代表扇形圆心角的度数。R代表这个扇形所在圆的半径。②L是扇形的弧长,R为半径。
锥形侧面积公式计算公式是Πr*l。关于锥形的计算公式 圆锥的侧面积=母线的平方×π×(360分之扇形的度数)==1/2×母线长×底面周长=π×底面圆的半径×母线。
圆锥侧面积的计算公式:圆锥的侧面积=(圆周率×母线长×圆心角度数)÷180。立体几何定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。旋转轴叫做圆锥的轴。