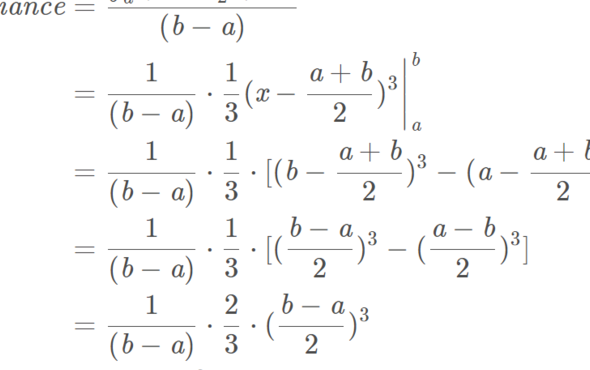均匀分布的数学期望与方差分别是多少呢?
若X服从[2,4]上的均匀分布,则数学期望EX=(2+4)/2=3;方差DX=(4-2)/12=1/3。
期望E(x)=(a+b)/2,方差D(x)=(b-a)/12。简单来说,均匀分布是指事件的结果是等可能的。掷骰子的结果就是一个典型的均匀分布,每次的结果是6个离散型数据,它们的发生是等可能的,都是1/6。
若X服从[2,4]上的均匀分布,则数学期望EX=(2+4)/2=3;方差DX=(4-2)/12=1/3。从任意分布抽样 均匀分布对于任意分布的采样是有用的。
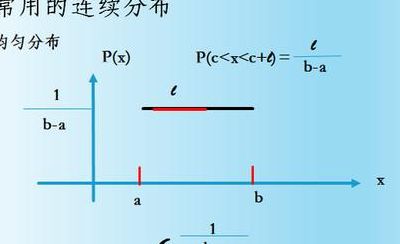
均匀分布在概率论和统计学中,均匀分布也叫矩形分布,它是对称概率分布,在相同长度间隔的分布概率是等可能的。均匀分布由两个参数a和b定义,它们是数轴上的最小值和最大值,通常缩写为U(a,b)。
均匀分布的期望和方差
1、均匀分布的期望:均匀分布的期望是取值区间[a,b]的中点(a+b)/2。
2、均匀分布的期望是取值区间[a,b]的中点(a+b)÷2,方差是var(x)=E[X2]-(E[X])2,数学期望是分布区间左右两端和的平均值。
3、期望E(x)=(a+b)/2,方差D(x)=(b-a)/12。简单来说,均匀分布是指事件的结果是等可能的。掷骰子的结果就是一个典型的均匀分布,每次的结果是6个离散型数据,它们的发生是等可能的,都是1/6。
4、均匀分布的方差:var(x)=E-(E),我们看看二阶原点矩E:因此,var(x)=E-(E)=1/3(a+ab+ b)-1/4(a+b)=1/12(a-2ab+ b)=1/12(a-b)。
5、均匀分布,期望是(a+b)/2,方差是(b-a)的平方/12。二项分布,期望是np,方差是npq。泊松分布,期望是p,方差是p。指数分布,期望是1/p,方差是1/(p的平方)。
6、六个常见分布的期望和方差:均匀分布,期望是(a+b)/2,方差是(b-a)的平方/12。二项分布,期望是np,方差是npq。泊松分布,期望是p,方差是p。指数分布,期望是1/p,方差是1/(p的平方)。
均匀分布的方差是什么样的?
均匀分布的方差:var(x)=E[X]-(E[X])。
均匀分布的期望:均匀分布的期望是取值区间[a,b]的中点(a+b)/2。均匀分布的方差:var(x)=E-(E)。重要分布的期望和方差:0-1分布:E(X)=p ,D(X)=p(1-p)。
均匀分布的方差:var(x)=E[X]-(E[X])var(x)=E[X]-(E[X])=1/3(a+ab+ b)-1/4(a+b)=1/12(a-2ab+ b)=1/12(a-b)。