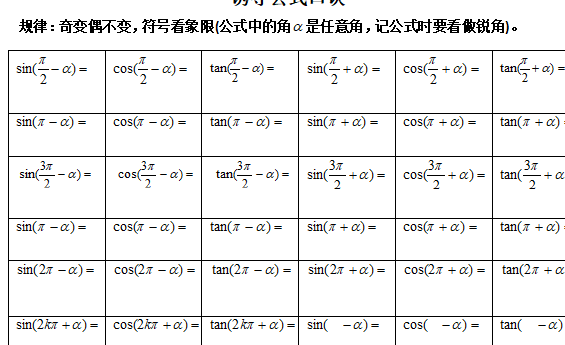
诱导公式的口诀是什么?
1、诱导公式口诀:“奇变偶不变,符号看象限”。“奇、偶”指的是π/2的倍数的奇偶,“变与不变”指的是三角函数的名称的变化:“变”是指正弦变余弦,正切变余切。
2、各种三角函数在四个象限的符号如何判断,也可以记住口诀:一全正;二正弦;三两切;四余弦。诱导公式:公式一:终边相同的角的同一三角函数的值相等。
3、诱导公式记忆口诀:“奇变偶不变,符号看象限”。诱导公式是数学三角函数中将角度比较大的三角函数利用角的周期性,转换为角度比较小的三角函数。
诱导公式的记忆口诀
奇变偶不变,符号看象限是诱导公式的口诀。奇变偶不变(对k而言,指k取奇数或偶数),符号看象限(看原函数,同时可把α看成是锐角)。
诱导公式口诀如下:诱导公式记忆口诀:“奇变偶不变,符号看象限”。“奇、偶”指的是r/2的倍数的奇偶,变与不变”指的是三角函数的名称的变化:变”是指正弦变余弦,正切变余切。
各种三角函数在四个象限的符号如何判断,也可以记住口诀:一全正;二正弦;三两切;四余弦。诱导公式:公式一:终边相同的角的同一三角函数的值相等。
诱导公式奇变偶不变,符号看象限是什么意思?
若是奇数,要变名,也就是sin变成cos,举例sin(π/2-α)=cosα 这里π/2的系数是1,奇数,所以等号右边要变名成为cosα。然后决定是cosα还是-cosα,也就是符号看象限。
“奇变偶不变,符号看象限”是三角函数诱导公式的记忆口诀,其中“奇变偶不变”是对k而言,指的是k取奇数或偶数;“符号看象限”指的是根据原函数判断正负,同时应把α看成是锐角。
“奇变偶不变”是说,角前面的度数是90度的倍数。
“奇变偶不变”可以理解为“纵变横不变”,即为当某角度(这里的α)前加减kπ+π/2 (这里的x)时,去掉或加上x的同时函数名要变,加减kπ就不变(k为整数)。
奇变偶不变,符号看象限是诱导公式的口诀。奇变偶不变(对k而言,指k取奇数或偶数),符号看象限(看原函数,同时可把α看成是锐角)。
诱导公式与旋转
1、诱导公式其实非常简单。首先说角度,加上一个角度就是逆时针旋转几度,减去呢,就是顺时针旋转。
2、诱导公式 (角度制)2诱导公式理解和记忆 奇变偶不边,符号看象限。(1)奇变偶不变。
3、如果是奇数 sin cos 互相变 tan cot互相变 偶数则 sin依然是sin 依次。符号看象限则把a不论为什么均看做锐角 最好利用直角坐标系 将这个锐角的终边进行旋转。如a-270.+则是逆时针转。-为顺时针转。
4、三角函数口诀 1三角函数在各象限的符号:一全正,二正弦,三正切,四余弦。2三角函数诱导公式口诀:公式1—5:函数名不变,符号看象限。公式1—6及推广:奇变偶不变,符号看象限。
5、当角度a为负数时,需要加上a。这是因为180度加减a的诱导公式是用来求得同一条直线上的对顶角的大小,而对顶角的大小取决于朝向角的正负性质。
6、诱导公式有0度~270度的9组诱导公式,90度=π。其他180度,360度,270度,根据公式1度等于π/180算。比如sin(-α)=-sinα。
诱导公式要记住什么口诀?
诱导公式口诀:“奇变偶不变,符号看象限”。“奇、偶”指的是π/2的倍数的奇偶,“变与不变”指的是三角函数的名称的变化:“变”是指正弦变余弦,正切变余切。
各种三角函数在四个象限的符号如何判断,也可以记住口诀:一全正;二正弦;三两切;四余弦。诱导公式:公式一:终边相同的角的同一三角函数的值相等。
诱导公式记忆口诀:“奇变偶不变,符号看象限”。诱导公式是数学三角函数中将角度比较大的三角函数利用角的周期性,转换为角度比较小的三角函数。
正弦诱导余弦,余弦诱导正弦,正切分母平方,余切分子平方。这句口诀可以帮助我们记忆正弦、余弦、正切和余切的诱导公式。
记忆方法:对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。诱导公式口诀:奇变偶不变,符号看象限。
公式右边的符号为把α视为锐角时,角k·360°+α(k∈Z),-α、180°±α,360°-α 所在象限的原三角函数值的符号可记忆 水平诱导名不变;符号看象限。
高中数学诱导公式口诀
1、高一诱导公式六个如下:公式一:sin(2kπ+α)=sinα(k∈Z)。cos(2kπ+α)=cosα(k∈Z)。tan(2kπ+α)=tanα(k∈Z)。公式二:sin(π+α)=-sinα。cos(π+α)=-cosα。
2、诱导公式口诀如下:诱导公式记忆口诀:“奇变偶不变,符号看象限”。“奇、偶”指的是r/2的倍数的奇偶,变与不变”指的是三角函数的名称的变化:变”是指正弦变余弦,正切变余切。
3、诱导公式口诀:“奇变偶不变,符号看象限”。诱导公式是数学三角函数中将角度比较大的三角函数利用角的周期性,转换为角度比较小的三角函数。
4、公式一: 设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα (k∈Z),cos(2kπ+α)=cosα (k∈Z),tan(2kπ+α)=tanα (k∈Z),cot(2kπ+α)=cotα(k∈Z)。