角动量和力矩的关系
角动量和力矩的关系是角动量定理M=dL/dt。力矩和角动量是物理学中常用的两个概念,它们的定义和计算方式是不同的,但它们之间有密切的关系。
角动量与力矩的关系如下:L定义为r与p的矢积,并不是非常直观的物理量这就是为了研究转动而人为定义的力学量。
某质点对参考系的角动量M对时间的变化率等于作用于该质点的合力对这个质点的力矩L,就是角动量定理,M=dL/dt。就是L对时间t的微分就是M,M和L都是有方向的。力矩 力矩表示力对物体作用时所产生的转动效应的物理量。
角动量定理又称动量矩定理。表述角动量与力矩之间关系的定理。对于质点,角动量定理可表述为:质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
刚体对轴的角动量L=Jω,刚体所受到的对某给定轴的总外力矩等于刚体对该轴的角动量的时间变化率,这是用角动量陈述的定轴转动定律。定轴转动物体对轴的角动量的增量等于外力对该轴的力矩的冲量之和。
角动量守恒定理 表述角动量与力矩之间关系的定理。对于质点,角动量定理可表述为:质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
角动量是什么定律?
首先需要了解,角动量(angular momentum) 在物理学中是和物体到原点的位移和动量相关的物理量。它表征质点矢径扫过面积速度的大小,或刚体定轴转动的剧烈程度。
角动量定理又称动量矩定理。表述角动量与力矩之间关系的定理。对于质点,角动量定理可表述为:质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
对于质点,角动量定理可表述为:质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。对于质点系,由于其内各质点间相互作用的内力服从牛顿第三定律,因而质点系的内力对任一点的主矩为零。
又称动量矩定理。表述角动量与力矩之间关系的定理。对于质点,角动量定理可表述为:质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
角动量定理公式是怎样的?
角动量定理公式:L = Jω,J 是转动惯量,ω(欧米伽)是角速度。角动量在经典力学中表示为到原点的位移和动量的叉乘,通常写做L 。角动量是矢量。
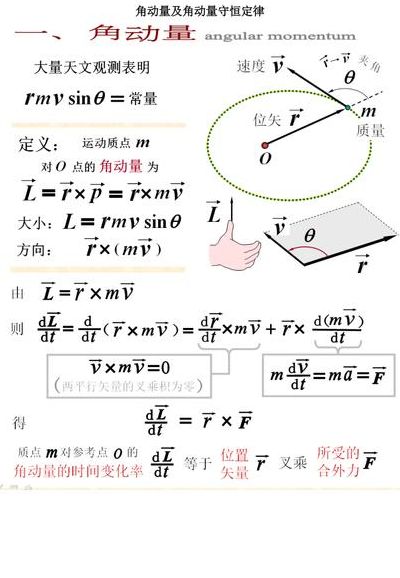
角动量的计算公式是L=r×p,其中r是质点相对O点的位矢,角动量L的大小为L=rpsinφ(φ为r与p的夹角),方向垂直于位矢r和动量p所组成的平面,指向是由r经小于180°的角转到p的右手螺旋前进的方向。
角动量定理公式:其中,r表示以质点到旋转中心(轴心)的距离(标量值可以理解为半径的大小),方向由原点指向物体位置的矢量(即矢径),L 表示角动量,v表示线速度,P表示动量,I表示惯性张量,w表示角速度(矢量)。
角动量定理是表述角动量与力矩之间关系的定理。对于质点,角动量定理可表述为:质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
角动量是物体旋转时的物理量,它的大小和方向都与物体的旋转状态有关。角动量的公式为:L = Iω 其中,L表示角动量,I表示物体的转动惯量,ω表示物体的角速度。角动量的单位是kg·m/s。
物理上讲的角动量定理是什么啊?
又称动量矩定理。表述角动量与力矩之间关系的定理。对于质点,角动量定理可表述为:质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
表述角动量与力矩之间关系的定理。对于质点,角动量定理可表述为:质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
角动量定理公式:L = Jω,J 是转动惯量,ω(欧米伽)是角速度。角动量在经典力学中表示为到原点的位移和动量的叉乘,通常写做L 。角动量是矢量。
角动量定理表述角动量与力矩之间关系的定理。对于质点,角动量定理可表述为:质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
角动量守恒的条件是
角动量守恒条件是合外力矩等于零。角动量守恒定律是物理学的普遍定律之一,反映质点和质点系围绕一点或一轴运动的普遍规律。如果合外力矩零(即M外=0),则L1=L2,即L=常矢量。
角动量守恒的条件是合外力的力矩为零。角动量守恒条件 对一固定点o,一个系统所受的合外力矩为零,则此质点的角动量矢量保持不变,即为一个系统角动量守恒的条件。物理学的普遍定律之一。
角动量守恒的条件就是和外力矩为零,动量守恒的条件是合外力为零。
质点系角动量守恒的条件是对一固定点o,一个系统所受的合外力矩为零,则此质点的角动量矢量保持不变,即为一个系统角动量守恒的条件。角动量守恒定律,条件-合外力矩等于零。
总之,角动量守恒定律的条件包括闭合系统、无外力作用、无摩擦力和对称性等方面。这些条件是保证角动量守恒的基础,只有在这些条件的基础上才能应用角动量守恒定律来解决实际问题。
什么是角动量守恒定律?
角动量守恒定律是物理学的普遍定律之一,反映质点和质点系围绕一点或一轴运动的普遍规律;反映不受外力作用或所受诸外力对某定点(或定轴)的合力矩始终等于零的质点和质点系围绕该点(或轴)运动的普遍规律。
角动量守恒定律:由刚体角动量定理式子可以看出,刚体角动量的变化源于刚体合外力矩的作用。当刚体所受合外力矩为零时,那么 L=Iw=恒量即当作定轴转动的刚体所受合外力矩为零时,刚体对转轴的角动量恒定不变。
对于质点,角动量定理可表述为:质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
角动量守恒定律是物理学的普遍定律之一,反映质点和质点系围绕一点或一轴运动的普遍规律。如果合外力矩零(即M外=0),则L1=L2,即L=常矢量。对一固定点o,质点所受的合外力矩为零,则此质点的角动量矢量保持不变。