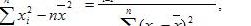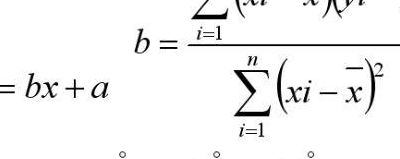回归直线方程
另有一种求a和b的“简捷”,其公式是:b=(n∑xy-∑x·∑y),回归直线法是根据若干期业务量和资金占用的历史资料,运用最小平方法原理计算不变资金a和单位产销量所需变动资金b。
在估计的直线回归方程为y=(x-x)/s+。其中,x是x的平均值,是y的平均值,s是样本标准差。这个公式实际上是将x变量进行了缩放,使得回归直线的斜率可以更好地反映x和y之间的线性关系。
x_^2=81/4 ,现在可以计算 b 了:b=(65-4*63/4) / (86-4*81/4)=0.7 ,而 a=y_-bx_=7/2-0.7*9/2=0.35 ,所以回归直线方程为 y=bx+a=0.7x+0.35 。
其中,且为观测值的样本方差.线性方程称为关于的线性回归方程,称为回归系数,对应的直线称为回归直线.顺便指出,将来还需用到,其中为观测值的样本方差。
回归直线法a,b的计算公式:b=(nΣxΣy-ΣxΣxy)/nΣx-(Σx)。a=(Σxy-bΣx)/n。
回归直线公式?
回归直线法的计算公式为:a=[∑Xi2∑Yi-∑Xi∑XiYi]/[n∑Xi2-(∑Xi)2],b=[n∑XiYi-∑Xi∑Yi]/[n∑Xi2-(∑Xi)2]。
直线回归方程公式如下:b=(n∑xiyi-∑xi·∑yi)÷[n∑xi2-(∑xi)^2],a=[(∑xi^2)∑yi-∑xi·∑xiyi]÷[n∑xi^2-(∑xi)^2],其中xi、yi代表已知的观测点。
回归直线法a,b的计算公式具体如下:回归直线法a,b的计算公式为b=(n∑xiyi-∑xi·∑yi)÷[n∑xi2-(∑xi)^2],a=[(∑xi^2)∑yi-∑xi·∑xiyi]÷[n∑xi^2-(∑xi)^2],其中xi、yi代表已知的观测点。
那个直线回归方程怎么求
要确定回归直线方程①,只要确定a与回归系数b。回归直线的求法通常是最小二乘法:离差作为表示xi对应的回归直线纵坐标y与观察值yi的差,其几何意义可用点与其在回归直线竖直方向上的投影间的距离来描述。
计算方法:回归直线的求法通常是最小二乘法:离差作为表示xi对应的回归直线纵坐标y与观察值yi的差,其几何意义可用点与其在回归直线竖直方向上的投影间的距离来描述。
依据两个变量之间的数据关系构建直线回归方程:Y=a+bx。 (其中:b=Lxy/Lxx a=y - bx) 一元线性回归方程的计算 步骤: 列计算表,求∑x,∑xx,∑y,∑yy,∑xy。
线性回归方程公式:b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)。线性回归方程是利用数理统计中的回归分析,来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法之一,应用十分广泛。
在估计的直线回归方程
在估计的直线回归方程为y=(x-x)/s+。其中,x是x的平均值,是y的平均值,s是样本标准差。这个公式实际上是将x变量进行了缩放,使得回归直线的斜率可以更好地反映x和y之间的线性关系。
回归直线方程公式为Yi-y^=Yi-a-bXi,离差作为表示Xi对应的回归直线纵坐标y与观察值Yi的差,其几何意义可用点与其在回归直线竖直方向上的投影间的距离来描述。
计算方法:回归直线的求法通常是最小二乘法:离差作为表示xi对应的回归直线纵坐标y与观察值yi的差,其几何意义可用点与其在回归直线竖直方向上的投影间的距离来描述。
另有一种求a和b的“简捷”,其公式是:b=(n∑xy-∑x·∑y),回归直线法是根据若干期业务量和资金占用的历史资料,运用最小平方法原理计算不变资金a和单位产销量所需变动资金b。
线性回归方程公式:b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)。线性回归方程是利用数理统计中的回归分析,来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法之一,应用十分广泛。
回归线方程公式解释
x_^2=81/4 ,现在可以计算 b 了:b=(65-4*63/4) / (86-4*81/4)=0.7 ,而 a=y_-bx_=7/2-0.7*9/2=0.35 ,所以回归直线方程为 y=bx+a=0.7x+0.35 。
线性回归方程公式:b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)。详解如下。第一:用所给样本求出两个相关变量的(算术)平均值。第二:分别计算分子和分母:(两个公式任选其一)分子。
线性回归方程r的计算公式是y = a + bx,其中y是被解释变量,x是解释变量,a是y截距,b是回归系数。这个模型的目的是找到对y有预测能力的最佳直线。在计算公式中,拟合的方程的系数a和b可以通过拟合样本数据来确定。
回归直线方程公式为Yi-y^=Yi-a-bXi,离差作为表示Xi对应的回归直线纵坐标y与观察值Yi的差,其几何意义可用点与其在回归直线竖直方向上的投影间的距离来描述。
回归线方程式怎么求
1、线性回归方程公式:b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)。线性回归方程是利用数理统计中的回归分析,来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法之一,应用十分广泛。
2、b的公式数学是:求回归线方程b公式:y=bx+a。回归方程是根据样本资料通过回归分析所得到的反映一个变量(因变量)对另一个或一组变量(自变量)的回归关系的数学表达式。
3、回归直线方程的一般形式是y=mx+b。其中m是斜率。b是截距。进行线性回归分析。得到斜率m和截距b的估计值。选择一个数据点(x。y)。将其代入y=mx+b中。解方程得到b=y-mx。
4、回归直线法a,b的计算公式:b=(nΣxΣy-ΣxΣxy)/nΣx-(Σx)。a=(Σxy-bΣx)/n。
5、这种使“离差平方和最小”的方法,叫做最小二乘法。用最小二乘法求回归直线方程中的a,b有图一和图二所示的公式进行参考。其中, 和 如图三所示,且 称为样本点的中心。