数学中的向量加法和减法的几句口诀.
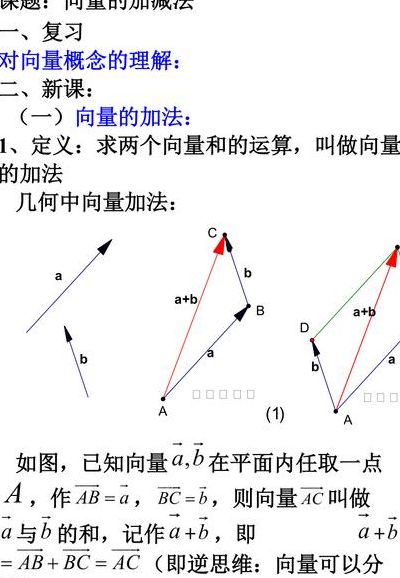
向量的加法口诀:首尾相连,首连尾,方向指向末向量。向量的减法口诀:首首相连,尾连尾,方向指向被减向量。三角形定则解决向量加减的方法 将各个向量依次首尾顺次相接,结果为第一个向量的起点指向最后一个向量的终点。
向量的加法满足平行四边形法则和三角形法则。AB+BC=AC。a+b=(x+x,y+y)。a+0=0+a=a。向量加法的运算律:交换律:a+b=b+a;结合律:(a+b)+c=a+(b+c)。
向量的加法 向量加法的运算律:交换律:a+b=b+a。结合律:(a+b)+c=a+(b+c)。向量的减法 如果a、b是互为相反的向量,那么a=-b,b=-a,a+b=0.0的反向量为0。AB-AC=CB.即“共同起点,指向被减”。a=(x,y) b=(x,y) 则 a-b=(x-x,y-y)。
向量加法
1、公式如下:向量的加法 向量的加法满足平行四边形法则和三角形法则。AB+BC=AC。a+b=(x+x,y+y)。a+0=0+a=a。向量加法的运算律:交换律:a+b=b+a;结合律:(a+b)+c=a+(b+c)。
2、在向量运算中,可以进行加法、减法、数乘和除法。下面简要介绍这些运算的计算方法: 向量加法 如果有两个向量 v = (v1, v2, v3) 和 w = (w1, w2, w3),它们的加法定义为 v + w = (v1 + w1, v2 + w2, v3 + w3)。即把对应位置的分量相加得到新的向量。
3、向量的加法 向量加法的运算律:交换律:a+b=b+a。结合律:(a+b)+c=a+(b+c)。向量的减法 如果a、b是互为相反的向量,那么a=-b,b=-a,a+b=0.0的反向量为0。AB-AC=CB.即“共同起点,指向被减”。a=(x,y) b=(x,y) 则 a-b=(x-x,y-y)。
4、向量相加怎么计算?参考如下:向量的加法 向量的加法是指将两个向量相加得到一个新向量的运算。向量的加法满足交换律和结合律。
向量加减法的方向怎么看?
向量AB+向量BC,首尾相接,取第一个的起点,最后一个终点。向量AC-向量AB,首相同,取第二个终点,第一个起点。一条线的起始点与另一条线的起始点连接是减。
向量的加法,箭头从第一加数向量的起点指向最末向量的终点。向量的减法,箭头从减数向量的起点指向被减向量的终点。若A箭头接B箭尾,则A+B为A箭尾指向B箭头,若A,B箭尾相接,则A_B为B箭头指向A箭头。
向量的加法 首尾相连,即第二个向量的起点连第一个向量的终点,得到的结果是,取第一个的起点,最后一个终点。即向量AB+向量BC=向量AC 向量减法 起点相同,被减向量的终点指向减向量的终点。得到的结果是取第二个终点,第一个起点。
y+y)、a+0=0+a=a。向量加法的运算律:交换律:a+b=b+a; 结合律:(a+b)+c=a+(b+c)。向量的减法 :如果a、b是互为相反的向量,那么a=-b,b=-a,a+b=0,0的反向量为0 。AB-AC=CB.即“共同起点,指向被减” ,a=(x,y) b=(x,y) 则 a-b=(x-x,y-y)。
向量减法的三角形法则:将两向量的始点(就是没箭头的那个点)放在一起,将两个终点连接,就是差,差向量方向指向被减向量。向量加法法则就是平行四边形法则,两个加数作为平行四边形相邻的两边,则和是两向量的公共顶点与对点相连的对角线。
向量的字母表示他的方向。减就是一端终点指向一端终点PA-PB=BA,如果不懂可以构建平行四边形。加就是一端起点只想一端终点AB+BC=AC。