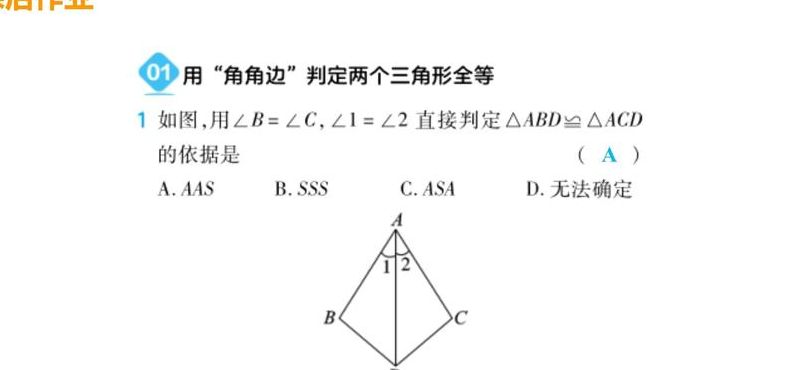
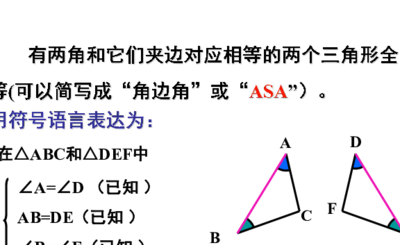
证明两个三角形全等的条件有哪些?
1、证明两个三角形全等的条件如下:两个三角形全等条件共有五种。边边边(SSS),三边相等。即如果有两个三角形,它们三条边都相等,则可以判断为两个三角形全等。边角边(SAS)两条边和它们间的夹角相等。即如果有两个三角形,两条边相等,并且他们间的夹角也相等,可以判断为两个三角形全等。
2、全等三角形共有5种判定方式:SSS、SAS、ASA、AAS、HL(只限直角三角形)。特殊情况下平移、旋转、对折也会构成全等三角形。SSS中文表示为“边边边”,指证明两个三角形全等的条件(三条边长度分别相等)。
3、两个三角形全等的条件有以下几种:SSS(边-边-边)法则、SAS(边-角-边)法则、ASA(角-边-角)法则、AAS(角-角-边)法则、RHS(直角-斜边-高)法则。SSS法则(边-边-边):当两个三角形的三条边分别相等时,这两个三角形是全等的。
判定三角形全等的条件
1、三角形全等的条件 (1)三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。(2)两边和它们的夹角对应相等的两个三角形全等,可以简写成“边角边”或“SAS”。(3)两角和它们的夹边对应相等的两个三角形全等,可以简写成“角边角”或“ASA”。
2、SSS:三个对应边相等的三角形全等。SAS:两边及其夹角对应相等的三角形全等。ASA:两角及其夹边对应相等的三角形全等。AAS:两角及其中一角的对边对应相等的三角形全等。HL:斜边和一条直角边对应相等的两个直角三角形全等。
3、两个三角形全等条件共有五种。边边边(SSS),三边相等。即如果有两个三角形,它们三条边都相等,则可以判断为两个三角形全等。边角边(SAS)两条边和它们间的夹角相等。即如果有两个三角形,两条边相等,并且他们间的夹角也相等,可以判断为两个三角形全等。
4、全等三角形的条件如下:边边边(SSS),三边相等。边角边(SAS)两条边和它们间的夹角相等。角边角(ASA)两个角它们间夹边相等。角角边(AAS)两个角和其中一角的边相等。直角三角形斜边和一条直角边相等(HL)。
5、全等三角形的条件是:首先SSS(边边边),即三边对应相等的两个三角形全等。然后SAS(边角边),即三角形的其中两条边对应相等且两条边的夹角也对应相等的两个三角形全等。ASA(角边角),即三角形的其中两个角对应相等且两个夹角的边也对应相等的两个三角形全等。
全等三角形的条件有哪些
1、三角形全等的条件 (1)三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。(2)两边和它们的夹角对应相等的两个三角形全等,可以简写成“边角边”或“SAS”。(3)两角和它们的夹边对应相等的两个三角形全等,可以简写成“角边角”或“ASA”。
2、全等三角形需要哪些条件如下:边相等的三角形全等 在最基础的层面上,已经知道如果两个三角形的三条边都相等,那么这两个三角形就是全等的。这一点的证明非常直接,只需要将两个三角形重叠在一起,然后检查是否所有的边和角都相等。
3、全等的三角形判定条件(六种),具体如下:定义法:两个完全重合的三角形全等。SSS:各三角形的三条边的长度都对应相等的话,该两个三角形就是全等三角形。
4、全等三角形的条件如下:边边边(SSS),三边相等。边角边(SAS)两条边和它们间的夹角相等。角边角(ASA)两个角它们间夹边相等。角角边(AAS)两个角和其中一角的边相等。直角三角形斜边和一条直角边相等(HL)。
5、全等三角形判定条件(六种)是:定义法:两个完全重合的三角形全等。SSS:三个对应边相等的三角形全等。SAS:两边及其夹角对应相等的三角形全等。ASA:两角及其夹边对应相等的三角形全等。AAS:两角及其中一角的对边对应相等的三角形全等。
6、两个三角形全等条件共有五种。边边边(SSS),三边相等。即如果有两个三角形,它们三条边都相等,则可以判断为两个三角形全等。边角边(SAS)两条边和它们间的夹角相等。即如果有两个三角形,两条边相等,并且他们间的夹角也相等,可以判断为两个三角形全等。