高中虚数i的知识点有哪些?
1、高中虚数i的知识点如下:虚数单位i,它的平方等于-1,即i2=-1。纯虚数当a=0且b0时的复数a+bi,即bi。复数a+bi的实部与虚部a叫做复数的实部,b叫做虚部(注意a,b都是实数)两个复数不能比较大小,只能由定义判断它们相等或不相等。
2、虚数单位 i 虚数单位 i 定义为 i^2 = -1。它是一个特殊的数,表示一个平方后得到负数的数。 复数 复数是由实数和虚数组成的数。一般形式为 a + bi,其中 a 是实部(实数部分),bi 是虚部(虚数部分)。复数可以表示为有序对 (a, b),其中 a 和 b 分别对应实部和虚部。
3、高中阶段学习虚数时,主要涉及以下几个知识点:虚数单位 i:虚数单位 i 定义为 i = -1。它是一个特殊的数,用来表示负的平方根。虚数单位 i 的引入扩展了实数系统,构成了复数集合。复数:复数是由实数和虚数构成的数。
4、高中虚数i的几个关键知识点包括: 虚数单位i,它的定义是平方等于-1,即i^2 = -1。 纯虚数是指实部为0的复数,形式为bi,其中b是一个非零实数。 复数a+bi由实部a和虚部b组成,其中a和b都是实数。 复数之间不能直接比较大小,但可以通过定义来判断它们是否相等。
5、复数高中知识点如下:复数的定义:复数是一个包含实部和虚部的数,一般形式为z=a+bi,其中a是实部,b是虚部,i是虚数单位,满足i^2=-1。复数的几何意义:复数可以用平面上的点来表示,实部为横坐标,虚部为纵坐标。复数的模表示该点到原点的距离,模长为√(a^2+b^2)。
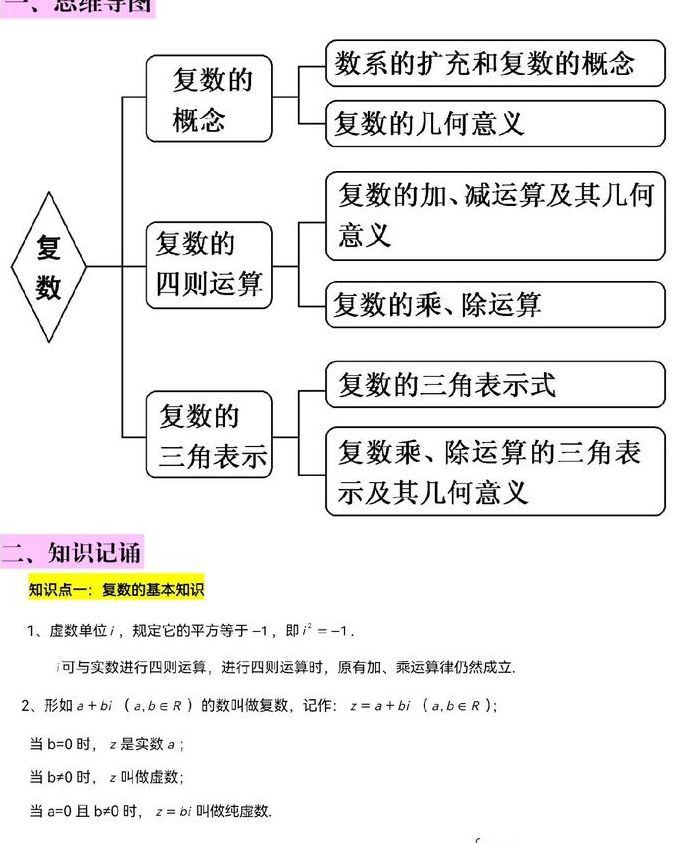
6、关于复数的知识点总结 知识网络图 复数中的。难点 (1)复数的向量表示法的运算。对于复数的向量表示有些学生掌握得不好,对向量的运算的几何意义的灵活掌握有一定的困难。对此应认真体会复数向量运算的几何意义,对其灵活地加以证明。(2)复数三角形式的乘方和开方。
高中数学虚数有哪些重要的知识点?
电路分析:虚数单位 i 在交流电路分析中起着重要的作用。通过将电流和电压表示为复数形式,可以方便地进行相量运算,求解电流和电压的幅值、相位等参数。 信号处理:虚数单位 i 也被广泛用于信号处理领域。通过将信号表示为复数形式,可以进行频域分析、滤波和信号变换等操作,例如傅里叶变换。
高中阶段学习虚数时,主要涉及以下几个知识点:虚数单位 i:虚数单位 i 定义为 i = -1。它是一个特殊的数,用来表示负的平方根。虚数单位 i 的引入扩展了实数系统,构成了复数集合。复数:复数是由实数和虚数构成的数。
高中虚数i的知识点如下:虚数单位i,它的平方等于-1,即i2=-1。纯虚数当a=0且b0时的复数a+bi,即bi。复数a+bi的实部与虚部a叫做复数的实部,b叫做虚部(注意a,b都是实数)两个复数不能比较大小,只能由定义判断它们相等或不相等。
高中虚数i的几个关键知识点包括: 虚数单位i,它的定义是平方等于-1,即i^2 = -1。 纯虚数是指实部为0的复数,形式为bi,其中b是一个非零实数。 复数a+bi由实部a和虚部b组成,其中a和b都是实数。 复数之间不能直接比较大小,但可以通过定义来判断它们是否相等。
高中数学共轭复数知识点
共轭复数:对于复数z=a+bi,称复数z=a-bi为z的共轭复数。即两个实部相等,虚部(虚部不等于0)互为相反数的复数互为共轭复数.复数z的共轭复数记作zˊ。表示方法为在字母z上方加一瞥线即共轭符号。如:︱x+yi︱=︱x-yi︱ 这和实数计算时有区别。
共轭复数,两个实部相等,虚部互为相反数的复数互为共轭复数。共轭复数,两个实部相等,虚部互为相反数的复数互为共轭复数(conjugate complex number)。当虚部不为零时,共轭复数就是实部相等,虚部相反,如果虚部为零,其共轭复数就是自身(当虚部不等于0时也叫共轭虚数)。
共轭复数,两个实部相等,虚部互为相反数的复数互为共轭复数。
是这样的,复数的共轭有如下性质:x共轭+y共轭=(x+y)共轭 因为(x+y)共轭,它的实部是x实部+y实部,它的虚部是x共轭的虚部+y共轭的虚部 x*x共轭=|x|^2 因为设x=a+bi,则x共轭=a-bi,由(a+bi)(a-bi)=a^2+b^2=|x|^2得 因此,这三步是成立的。
高中数学复数讲解
纯虚数:当实部为0时,仅剩的虚部为纯虚数,如:当a=0且b≠0时,z=bi,我们就将其称为纯虚数。共轭复数:对于复数z=a+bi,称复数z=a-bi为z的共轭复数。即两个实部相等,虚部(虚部不等于0)互为相反数的复数互为共轭复数.复数z的共轭复数记作zˊ。
复数高中知识点如下:复数的定义:复数是一个包含实部和虚部的数,一般形式为z=a+bi,其中a是实部,b是虚部,i是虚数单位,满足i^2=-1。复数的几何意义:复数可以用平面上的点来表示,实部为横坐标,虚部为纵坐标。复数的模表示该点到原点的距离,模长为√(a^2+b^2)。
纯复数是复数的一种,即复数是由纯复数与非纯复数构成。复数的基本形式为a+bi。其中a和b为实数,i为虚数单位,其平方为-1。共轭复数,两个实部相等,虚部互为相反数的复数互为共轭复数。