几何布朗运动
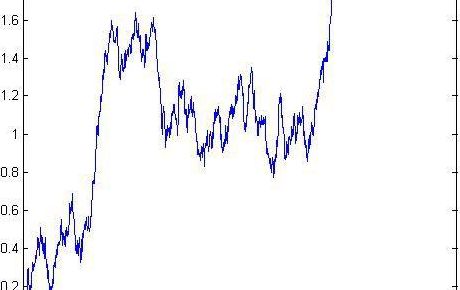
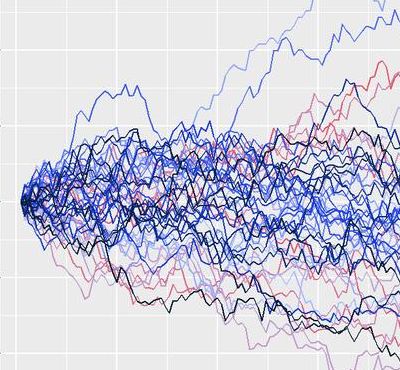
几何布朗运动的作用是用来模拟股价的变动。它的好处在于,一般形式布朗运动中取值可能为负数,而几何布朗运动取值永远不小于0,这一点符合股价永远不为负的特征。几何布朗运动微分形式的表述。
几何布朗运动是指一群粒子在随机方向上的运动,其轨迹呈现出几何形状。这种运动具有许多有趣的性质,如随机性、不确定性和模糊性,因此它在物理学、化学、生物学等领域中都有广泛的应用。
几何布朗运动是宽平稳过程。布朗运动是正交增量过程的一种典例。并且布朗运动通过某些变换,也可以变成宽平稳随机过程,因此几何布朗运动是宽平稳过程。
最大值减去最小值。根据查询几何布朗运动相关资料显示,几何布朗运动的期望和方差是最大值减去最小值。几何布朗运动 (GBM)(也叫做指数布朗运动)是连续时间情况下的随机过程,其中随机变量的对数遵循布朗运动。
没听过几何布朗运动貌似有布朗运动和布朗实验悬浮微粒不停地做无规则运动的现象叫做布朗运动这是1826年英国植物学家布朗(1773-1858)用显微镜观察悬浮在水中的花粉是发现的。后来把悬浮微粒的这种运动叫做布朗运动。
几何布朗运动是什么?
1、几何布朗运动是指一群粒子在随机方向上的运动,其轨迹呈现出几何形状。这种运动具有许多有趣的性质,如随机性、不确定性和模糊性,因此它在物理学、化学、生物学等领域中都有广泛的应用。
2、几何布朗运动的作用是用来模拟股价的变动。它的好处在于,一般形式布朗运动中取值可能为负数,而几何布朗运动取值永远不小于0,这一点符合股价永远不为负的特征。几何布朗运动微分形式的表述。
3、布朗发现水中的花粉及其它悬浮的微小颗粒不停地作不规则的折线运动,称为布朗运动。人们长期都不知道其中的原理。50年后,J·德耳索提出这些微小颗粒是受到周围分子的不平衡的碰撞而导致的运动。后来得到爱因斯坦的研究的证明。
几何布朗运动和分数布朗运动有什么区别
1、布朗运动(Brownian motion)是一种正态分布的独立增量连续随机过程。它是随机分析中基本概念之一。其基本性质为:布朗运动W(t)是期望为0方差为t(时间)的正态随机变量。
2、几何布朗运动的作用是用来模拟股价的变动。它的好处在于,一般形式布朗运动中取值可能为负数,而几何布朗运动取值永远不小于0,这一点符合股价永远不为负的特征。几何布朗运动微分形式的表述。
3、对称性:普通布朗运动具有空间和时间上的对称性,而标准布朗运动没有这样的对称性。 物理应用:普通布朗运动常用于描述悬浮在流体中的微粒的运动,而标准布朗运动则不具有这种物理应用。
4、对寻常布朗运动H=1/2,是完全随机的;当它不等于1/2时,这时的布朗运动就叫做分形布朗运动(fBM),这时的运动不是完全随机的,具有长程相关性。具体说来,就是0<H<1/2时具有反相关性,1/2<H<1时具有正相关性。
几何布朗运动的期望和方差怎么求
1、其基本性质为:布朗运动W(t)是期望为0方差为t(时间)的正态随机变量。对于任意的r小于等于s,W(t)-W(s)独立于的W(r),且是期望为0方差为t-s的正态随机变量。
2、它的期望为1/p,方差为(1-p)/(p的平方)。求几何分布的期望公式:Eε=1/p。在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。
3、几何分布的期望和方差公式分别是E(n)等于1/p、E(m)等于(1-p)/p,几何分布是离散型概率分布。其中一种定义为:在n次伯努利试验中,试验k次才得到第一次成功的机率。详细地说,是:前k-1次皆失败,第k次成功的概率。
4、标准布朗运动期望求的方法是:使用公式。公式分别为:期望E(X)=a×p1+b×p2+cp3。方差f等于最大值减去最小值。
5、几何分布的期望和方差公式分别是E(n)=1/p、E(m)=(1-p)/p。几何分布是离散型概率分布,其中一种定义为前k-1次皆失败,第k次成功的概率。
6、你好!根据性质,它们和的方差等于各变数方差之和,每个几何分布的方差是(1-p)/p^2,所以总的方差是n(1-p)/p^2。经济数学团队帮你解请及时采纳。