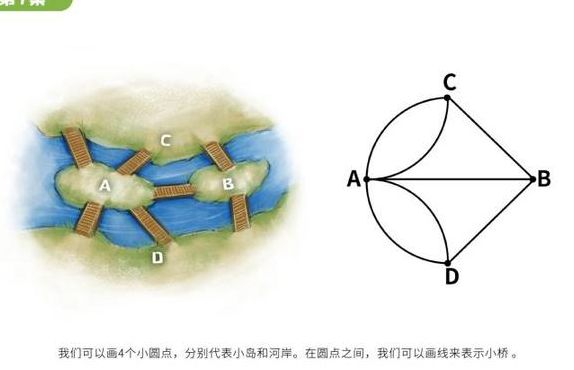
什么是七桥问题?
答案是无解的,你要记住,七桥问题即:能否笔不离纸,不重复地一笔画完整个图形。“一笔画”问题,数学分析:一笔画有起点和终点,起点和终点重合的图形称为封闭图形,否则便称为开放图形。
除起点和终点外,一笔画中间可能出现一些曲线的交点。只有当笔沿着一条弧线到达交点后,又能沿着另一条弧线离开,也就是交汇于这些点的弧线成双成对时,一笔画才能完成,这样的交点就称为“偶点”。
如果交汇于这些点的弧线不是成双成对,也就是有奇数条,则一笔画就不能实现,这样的点又叫做“奇点”
结论:若是一个一笔画图形,要么只有两个奇点,也就是仅有起点和终点,这样一笔画成的图形是开放的;要么没有奇点,也就是终点和起点连接起来,这样一笔画成的图形是封闭的。由于七桥问题有四个奇点,所以要找到一条经过七座桥,但每座桥只走一次的路线是不可能的。
七桥问题的最简单解法?
最简单的解法是使用回溯法,它使用递归搜索方法来尝试每一种可能的解,然后检查每个解是否满足要求。
在每一步中,算法考虑添加一个新的桥,如果它不会使得桥梁形成环,则可以接受。如果算法找到了一条满足要求的桥梁,则可以接受该解。否则,它会继续搜索,直到找到可行解为止。
七桥问题的规律及解法?
七桥问题是著名的数学问题,也被称为哥尼斯堡七桥问题,由欧拉在18世纪提出。问题描述如下:欧拉在哥尼斯堡的市区地图上画了一个图,图上有一座小岛,岛与两岸分别通过七座桥连接。欧拉的问题是,是否可以从起点开始,经过每座桥一次,最后回到起点。
规律:
- 对于任何一个图,如果某个节点的度数(连接的边数)为奇数,那么必定存在一个欧拉路径(可以经过每条边一次且只经过一次的路径)或欧拉回路(经过每条边一次且回到起点的路径)。
- 对于连通的图,如果所有节点的度数都是偶数,那么存在欧拉回路,也就是可以从某个节点出发经过每条边一次且回到起点。
- 对于连通的图,如果有两个以上的节点的度数是奇数,那么不存在欧拉路径或欧拉回路。
解法:
根据以上规律,对于七桥问题的具体情况进行分析:
- 每个岛和岸的连接桥都是偶数个,所以所有节点的度数都是偶数。
- 有两个以上的节点的度数是奇数(起点和终点两个岸),因此在这个问题中不存在欧拉路径或欧拉回路。
因此,哥尼斯堡七桥问题无解。
需要注意的是,七桥问题的规律和解法可用于其他类似的问题,对于更为复杂的图论问题,可能需要利用更深入的图论知识和算法进行分析。
七桥问题有一个规律,即在一个图形中,如果连接的边数为奇数个的节点个数为偶数,那么这个图形是可以一笔画的。
但如果连接的边数为奇数个的节点个数为奇数,那么这个图形是无法一笔画的。
七桥问题最早由欧拉提出,他通过数学方法证明了这个规律。
他把问题抽象化,将桥和岛屿用点表示,将桥连接岛屿的线段用边表示,然后分析了图形的特征,得出了这个规律。
对于解法,可以通过思考把图形转化为具有奇数节点个数的情况,例如添加一个虚拟节点,使节点个数变为偶数。
然后按照上述规律一笔画即可。
值得注意的是,七桥问题仅适用于二维平面,且要求边不能重叠。
在更高维度的情况下,类似的规律可能会变得更为复杂。