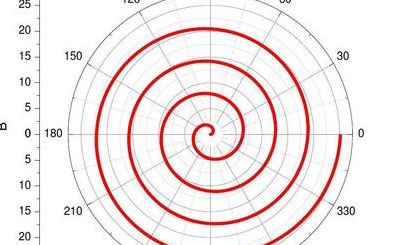
阿基米德螺线方程
阿基米德螺旋线参数方程:1)极坐标参数方程为:r = aθ 2)笛卡尔坐标下的参数方程式为:r=x*(1+t)x=r*cos(t * 360)y=r*sin(t *360)z=0 阿基米德螺线(阿基米德曲线) ,亦称“等速螺线”。
阿基米德螺线的极坐标方程式为:其中 a 和 b 均为实数。改变参数 a相当于旋转螺线线,而参数 b 则控制相邻两条曲线之间的距离。
阿基米德螺线(阿基米德曲线) ,亦称“等速螺线”。当一点P沿动射线OP以等速率运动的同时,这射线有以等角速度绕点O旋转,点P的轨迹称为“阿基米德螺线”。
阿基米德螺线是什么?
1、阿基米德螺线(亦称等速螺线),得名于公元前三世纪希腊数学家阿基米德。阿基米德螺线是一个点匀速离开一个固定点的同时又以固定的角速度绕该固定点转动而产生的轨迹。阿基米德在其著作《螺旋线》中对此作了描述。
2、阿基米德螺线在机械凸轮设计中有广泛的应用。
3、阿基米德螺线 是所有形式为 (极坐标方程)r = aθ 的螺线。这种螺线的每条臂的距离永远相等于 2πa。
4、阿基米德螺线 ,亦称“等速螺线”。当一点P沿动射线OP一等速率运动的同时,这射线有以等角速度绕点O旋转,点P的轨迹称为“阿基米德螺线”。它的极坐标方程为:r = aθ这种螺线的每条臂的距离永远相等于 2πa。
什么是阿基米得线
1、阿基米德螺线(亦称等速螺线),得名于公元前三世纪希腊数学家阿基米德。阿基米德螺线是一个点匀速离开一个固定点的同时又以固定的角速度绕该固定点转动而产生的轨迹。阿基米德在其著作《螺旋线》中对此作了描述。
2、所谓阿基米德螺线,是指一个动点匀速离开一个定点的同时又以固定的角速度绕该定点转动而产生的轨迹。其中,定点就是位置固定的点,不会移动。动点就是位置会发生移动的点。匀速,就是均匀的速度。
3、阿基米德螺线(亦称等速螺线),得名于公元前三世纪希腊数学家阿基米德。阿基米德螺线是一个点匀速离开一个固定点的同时又以固定的角速度绕该固定点转动而产生的轨迹。阿基米德在其著作《螺旋线》中对此作了描述。
阿基米德螺旋线是什么?(极坐标方程)又是什么?
1、阿基米德螺线(阿基米德曲线),亦称“等速螺线”。当一点p沿动射线op以等速率运动的同时,这射线有以等角速度绕点o旋转,点p的轨迹称为“阿基米德螺线”。
2、阿基米德螺线 是所有形式为 (极坐标方程)r = aθ 的螺线。这种螺线的每条臂的距离永远相等于 2πa。
3、词典解释 :又称“等速螺线”。当一动点沿极径作匀速直线运动,极径又作匀角速旋转时动点的轨迹。设动点的初始位置到极点o的距离为ρ0,则螺线的极坐标方程为ρ=ρ0+aθ,其中a为常数。